
已知抛物线 (
( )与
)与 轴相交于点
轴相交于点 ,顶点为
,顶点为 .直线
.直线 分别与
分别与 轴,
轴, 轴相交于
轴相交于 两点,并且与直线
两点,并且与直线 相交于点
相交于点 .
.
(1)如图,将 沿
沿 轴翻折,若点
轴翻折,若点 的对应点
的对应点 ′恰好落在抛物线上,
′恰好落在抛物线上, ′与
′与 轴交于点
轴交于点 ,连结
,连结 ,求
,求 的值和四边形
的值和四边形 的面积;
的面积;

(2)在抛物线 (
( )上是否存在一点
)上是否存在一点 ,使得以
,使得以 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
(1) ,
, ;(2)
;(2) 或
或
【解析】
试题分析:(1)先求得 ,由题意得点
,由题意得点 与点
与点 ′关于
′关于 轴对称,即可得到点
轴对称,即可得到点 ′的坐标,从而求得a的值,即得点
′的坐标,从而求得a的值,即得点 到
到 轴的距离为3,再根据待定系数法求得直线
轴的距离为3,再根据待定系数法求得直线 的解析式,再求得它与
的解析式,再求得它与 轴的交点坐标,即可得到四边形
轴的交点坐标,即可得到四边形 的面积;
的面积;
(2)当点 在
在 轴的左侧时,若
轴的左侧时,若 是平行四边形,则
是平行四边形,则 平行且等于
平行且等于 ,则把
,则把 向上平移
向上平移 个单位得到
个单位得到 ,坐标为
,坐标为 ,代入抛物线的解析式即可求得点P的坐标;当点
,代入抛物线的解析式即可求得点P的坐标;当点 在
在 轴的右侧时,若
轴的右侧时,若 是平行四边形,则
是平行四边形,则 与
与 互相平分,即可得到点P的坐标.
互相平分,即可得到点P的坐标.
(1)
由题意得点 与点
与点 ′关于
′关于 轴对称,
轴对称,
 ,
,
将 ′的坐标代入
′的坐标代入 得
得 ,
,
 (舍去),
(舍去),
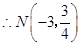 ,
, 点
点 到
到 轴的距离为3.
轴的距离为3.
 ,
,
 ,
, 直线
直线 的解析式为
的解析式为 ,
,
它与 轴的交点为
轴的交点为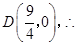 点
点 到
到 轴的距离为
轴的距离为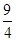 .
.

(2)当点 在
在 轴的左侧时,若
轴的左侧时,若 是平行四边形,则
是平行四边形,则 平行且等于
平行且等于 ,
,
 把
把 向上平移
向上平移 个单位得到
个单位得到 ,坐标为
,坐标为 ,代入抛物线的解析式,
,代入抛物线的解析式,
得:
 (不舍题意,舍去),
(不舍题意,舍去), ,
,
当点 在
在 轴的右侧时,若
轴的右侧时,若 是平行四边形,则
是平行四边形,则 与
与 互相平分,
互相平分,
 .
.
 与
与 关于原点对称,
关于原点对称,
 ,
,
将 点坐标代入抛物线解析式得:
点坐标代入抛物线解析式得: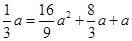 ,
,
 (不合题意,舍去),
(不合题意,舍去), ,
, .
.
 存在这样的点
存在这样的点 或
或 ,能使得以
,能使得以 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:初中数学 来源: 题型:
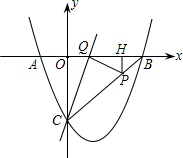 如图,已知抛物线y=
如图,已知抛物线y=| 3 |
| 4 |
| 3 |
| 4t |
| 2 |
| 7 |
| 32 |
| 25 |
| 32 |
| 2 |
| 7 |
| 32 |
| 25 |
| 32 |
查看答案和解析>>
科目:初中数学 来源:2010年浙江省初中毕业生学业考试适应性监测考试数学试卷(解析版) 题型:解答题
 +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH= .
. =
= 时,求点P的坐标;
时,求点P的坐标;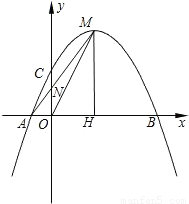
查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市五月调考九年级数学试卷(解析版) 题型:解答题
 +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=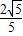 .
. =
= 时,求点P的坐标;
时,求点P的坐标;
查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市教育科学研究院命制中考数学模拟试卷(解析版) 题型:解答题
 +c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH= .
. =
= 时,求点P的坐标;
时,求点P的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com