
| A. | 7π,24π,25π | B. | $\frac{5}{4}$,1,$\frac{3}{4}$ | C. | 0.1,0.2,0.3 | D. | $\sqrt{2}$,1,$\sqrt{3}$ |
分析 根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个三角形就不是直角三角形.
解答 解:A、(7π)2+(24π)2=(25π)2,符合勾股定理的逆定理,能作为直角三角形三边长,故本选项不符合题意;
B、12+($\frac{3}{4}$)2=($\frac{5}{4}$)2,符合勾股定理的逆定理,能作为直角三角形三边长,故本选项不符合题意;
C、0.12+0.22≠0.32,不符合勾股定理的逆定理,不能作为直角三角形三边长,故本选项符合题意;
D、($\sqrt{2}$)2+12=($\sqrt{3}$)2,符合勾股定理的逆定理,能作为直角三角形三边长,故本选项不符合题意.
故选C.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
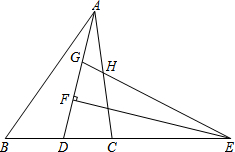 如图,在△ABC中,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.
如图,在△ABC中,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
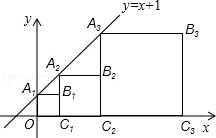 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是( )| A. | (63,32) | B. | (64,32) | C. | (63,31) | D. | (64,31) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{2}{5}}$ | B. | $\sqrt{x^2}$ | C. | $\sqrt{0.3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
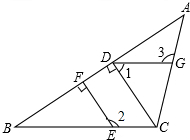 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.
如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com