
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC= ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
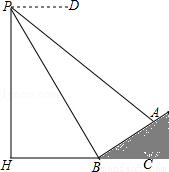
(1)求∠ABP的度数;
(2)求A,B两点间的距离.
解:(1)∵tan∠ABC=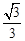 ,∴∠ABC=30°。
,∴∠ABC=30°。
∵从P点望山脚B处的俯角60°,∴∠PBH=60°。
∴∠ABP=180°﹣30°﹣60°=90°。
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,∴∠ABP=90°。
又∵∠APB=30°,∴△PAB为等腰直角三角形。
在Rt△PHB中,PB=PH•tan∠PBH=300 .
.
在Rt△PBA中,AB=PB•tan∠BPC=300。
∴A、B两点之间的距离为300米
【解析】
试题分析:(1)根据俯角以及坡度的定义即可求解。
(2)在Rt△PHB中,根据三角函数即可求得PB的长,然后在Rt△PBA中利用三角函数即可求解。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
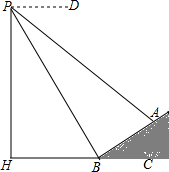 (2013•赤峰)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=
(2013•赤峰)如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
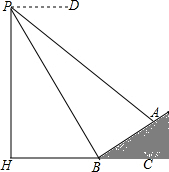 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC= ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.查看答案和解析>>
科目:初中数学 来源:2013年内蒙古赤峰市中考数学试卷(解析版) 题型:解答题
 如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC=
如图,数学实习小组在高300米的山腰(即PH=300米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°.已知tan∠ABC= ,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.
,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且PH⊥HC.查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com