
以原点O为圆心,1cm为半径的圆分别交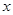 、
、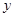 轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
轴的正半轴于A、B两点,点P的坐标为(2,0),动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设运动的时间为秒.
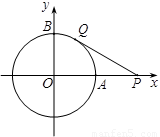
(1)如图一,当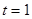 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留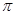 );
);
(2)若点Q按照(1)中的速度继续运动.
①当为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.
(1)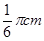 /秒;(2)①
/秒;(2)①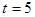 ,
,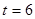 或
或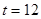 ;②
;②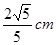
【解析】
试题分析:(1)连接OQ,则OQ⊥PQ,OQ=1,OP=2,所以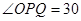 °,即
°,即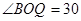 °,再根据弧长公式即可求得弧BQ的长,从而得到点Q的运动速度;
°,再根据弧长公式即可求得弧BQ的长,从而得到点Q的运动速度;
(2)①由(1)可知,当t=1时,△OPQ为直角三角形,所以,当Q'与Q关于x轴对称时,△OPQ'为直角三角形,此时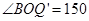 °,
°, ,
,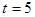 ,再结合当Q'(0,-1)或Q'(0,1)时求解即可;
,再结合当Q'(0,-1)或Q'(0,1)时求解即可;
②当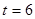 或
或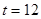 时,直线PQ与⊙O相交.作OM⊥PQ,根据等面积法及勾股定理可求得PM的长,从而求的结果.
时,直线PQ与⊙O相交.作OM⊥PQ,根据等面积法及勾股定理可求得PM的长,从而求的结果.
(1)连接OQ,
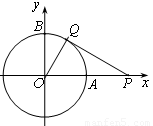
则OQ⊥PQ,OQ=1,OP=2,所以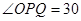 °,即
°,即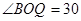 °,
°,
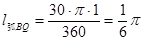 ,所以点Q的运动速度为
,所以点Q的运动速度为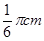 /秒;
/秒;
(2)①由(1)可知,当t=1时,△OPQ为直角三角形,所以,当Q'与Q关于x轴对称时,△OPQ'为直角三角形,此时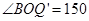 °,
°, ,
,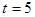 ,
,
当Q'(0,-1)或Q'(0,1)时,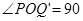 °,此时
°,此时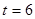 或
或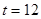 ,
,
即当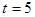 ,
,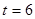 或
或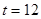 时,△OPQ是直角三角形;
时,△OPQ是直角三角形;
②当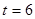 或
或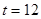 时,直线PQ与⊙O相交.作OM⊥PQ,根据等面积法可知:
时,直线PQ与⊙O相交.作OM⊥PQ,根据等面积法可知:
PQ×OM=OQ×OP,PQ=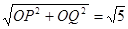 ,
,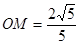 ,
,
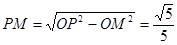 ,弦长
,弦长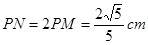 .
.
考点:动点综合题
点评:动点的综合题是初中数学的重点和难点,在中考中极为常见,一般压轴题形式出现,难度较大.


科目:初中数学 来源: 题型:
 如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是( )
如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是( )| A、-1≤x<0或0<x≤1 | ||||
| B、0<x≤1 | ||||
C、-
| ||||
| D、x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是
如图,已知⊙O是以数轴的原点为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OB平行的直线于⊙O有公共点,设P(x,0),则x的取值范围是 ≤x<0或0<x≤
≤x<0或0<x≤
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江西省上饶市鄱阳县九年级(上)期末数学试卷(解析版) 题型:选择题

 ≤x<0或0<x≤
≤x<0或0<x≤
查看答案和解析>>
科目:初中数学 来源:2010-2011学年江西省南昌市九年级(上)期末数学试卷(解析版) 题型:选择题

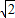 ≤x<0或0<x≤
≤x<0或0<x≤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com