
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
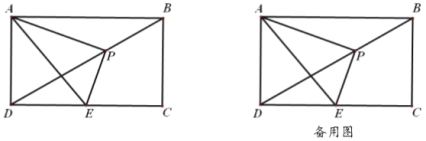
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值;
的值;
(3)在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)见解析;(2)DE为![]() ;(3)BP的值为
;(3)BP的值为![]()
【解析】
(1)根据矩形性质得到∠ADC=90°,在四边形ADEP中根据内角和定理得到∠DEP+∠DAP=180°,再根据同角的余角相等即可证明;
(2)连接AC,求出∠ADB=60°,证明△ADP为等边三角形,证明Rt△ADE≌Rt△APE,求出∠DAE=∠PAE=30°,根据![]() ,即可求出DE;
,即可求出DE;
(3)过点P作PG⊥AB于G,GP的延长线交DC于H,设PG=a,AG=![]() ,EH=
,EH= ![]() ,证明△AGP∽△PHE,得到
,证明△AGP∽△PHE,得到![]() ,构造关于a的方程,解方程即可.
,构造关于a的方程,解方程即可.
(1)证明:∵PE⊥AP,∴∠APE=90°;
∵四边形ABCD是矩形
∴∠ADC=90°
在四边形ADEP中
∠ADE+∠DEP+∠APE+∠DAP=360°
∴∠DEP+∠DAP=360°-90°-90°=180°
又∵∠DEP+∠PEC=180°
∴∠PAD=∠PEC
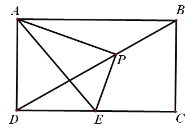
(2)连接AC,
∵四边形ABCD是矩形,AB=![]() ,AD=2;
,AD=2;
∴![]()
∴∠ADB=60°
∵当点P是BD的中点
∴点P为AC与BD的交点
∴△ADP为等边三角形
∴AP=AD=2
在Rt△ADE和Rt△APE中
![]()
∴Rt△ADE≌Rt△APE(HL)
∴∠DAE=∠PAE=30°
∴![]()
∴![]()
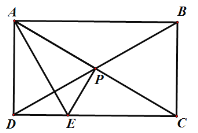
答:DE为![]()
(3)如图,过点P作PG⊥AB于G,GP的延长线交DC于H,四边形ABCD是矩形
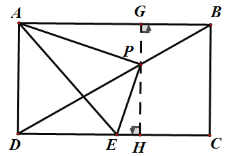
∴PG⊥DC,
∴GH=BC=2,
设PG=a,则PH=GH﹣PH=2﹣a,
在Rt△BGP中,
tan∠PBG=![]() ,
,
∴BG=![]() PG=
PG=![]() a,
a,
∴AG=AB﹣BG=2![]() ﹣
﹣![]() a=
a=![]() (2﹣a),
(2﹣a),
EH=DH-DE=2![]() ﹣
﹣![]() a﹣
a﹣![]() =
=![]() ﹣
﹣![]() a
a
∵PG⊥DC,
∴∠APG+∠EPH=90°,
∵∠APG+∠PAG=90°,
∴∠EPH=∠PAG,
∵∠AGP=∠PHE=90°,
∴△AGP∽△PHE,
∴![]() ,
,
![]()
![]()
∴BP=2PG=![]()
答:BP的值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
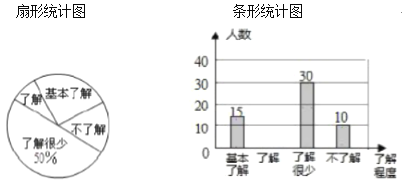
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
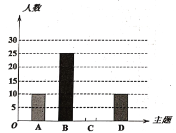
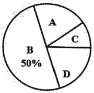
【题目】某校开展了“创建文明校园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)请你补全条形统计图;
(3)在扇形统计图中,“A”所在扇形的圆心角等于 度;
(4)小明和小华各自随机参加其中的一个主题活动,请用画树状图或列表的方式,求他们恰好同时选中“文明礼仪”或“生态环境”主题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.

(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
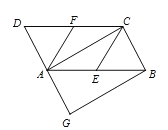
【题目】如图,在平行四边形ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
(1)求证:△ADF≌△CBE;
(2)若四边形AGBC是矩形,判断四边形AECF是什么特殊的四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“生物”学科学生的学习状况,某校从七年级学生中随机抽取了部分学生进行测试,测试结果分为四个等级:![]() :优秀,
:优秀,![]() :良好,
:良好,![]() :及格,
:及格,![]() :不及格,并将结果绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:
:不及格,并将结果绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:
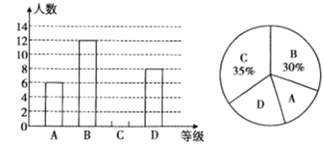
(1)共抽取了多少名学生进行测试?
(2)通过计算补全条形统计图;
(3)该校七年级学生共有450名学生,请你估计该校“生物”学科不及格的学生人数是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com