
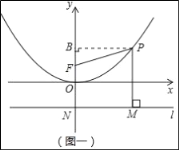
����Ŀ����ͼ����PΪ������y=![]() x2��һ���㣮
x2��һ���㣮
��1����������y=![]() x2����������y=
x2����������y=![]() ��x+2��2��1ͨ��ͼ��ƽ�Ƶõ��ģ���д��ƽ�ƵĹ��̣�
��x+2��2��1ͨ��ͼ��ƽ�Ƶõ��ģ���д��ƽ�ƵĹ��̣�
��2����ֱ��l����y����һ��N����ƽ����x�ᣬ��N������Ϊ��0����1��������P��PM��l��M��
������̽������ͼһ���ڶԳ������Ƿ����һ����F��ʹ��PM=PF������������ڣ������F�����꣺�������ڣ���˵�����ɣ�
������������ͼ��������Q������Ϊ��1.5������QP+PF����Сֵ��

���𰸡���1������ƽ��1����λ��������2����λ����2������0��1������5
����������1���ҵ������߶������꼴���ҵ�ƽ�Ʒ�ʽ��
��2���������P���꣬����PM=PF����BF�����F���ꣻ
������PM=PF����QP+PFת��ΪQP+QM�����ô��߶���̽�����⣮
��1����������![]() �Ķ���Ϊ����2����1��
�Ķ���Ϊ����2����1��
��������![]() ��ͼ������ƽ��1����λ��������2����λ�õ�������
��ͼ������ƽ��1����λ��������2����λ�õ�������![]() ��ͼ��
��ͼ��
��2���ٴ���һ����F��ʹ��PM=PF�������
��ͼһ������P��PB��y���ڵ�B
���P����Ϊ![]() ,
,
��![]() ,
,
��![]()
��![]() ��
��
![]()
��OF=1
���F������0��1��
���ɢ���PM=PF��
![]() ����СֵΪ
����СֵΪ![]() ����Сֵ
����Сֵ
��Q��P��M���㹲��ʱ��QP+QM����СֵΪ��Q������5��
��QP+PF����СֵΪ5��


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η��� ![]() ��ʵ������
��ʵ������
��1����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���� ����ʵ�����ֱ�Ϊ ![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѽ�ij������9ʱ�����г��뿪�ң�17ʱ�ؼң��������������ҵľ�����ʱͬ�ı仯�������ͼ��ʾ.
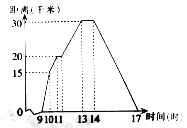
��1��ͼ���ʾ�������������Ĺ�ϵ��
��2��10ʱ��11ʱ�����ֱ���Ҷ�Զ��
��3����������������Զ�ĵط���ʲôʱ�䣿��Ҷ�Զ��
��4��11ʱ��13ʱ����ʻ�˶���ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� Rt��ABC �У���BAC=90����AC=AB���� F ������ CA ��һ�㣬���� BF���� C �� CE��BF������Ϊ�� E��ֱ�� CE��AB �ཻ�ڵ� D��
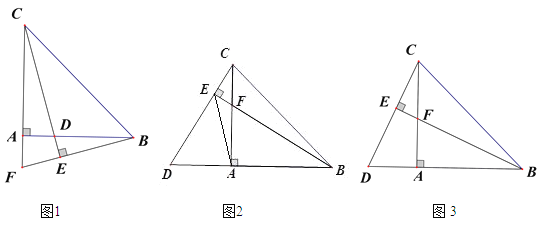
��1����ͼ 1������ F ���߶� CA �ӳ�����ʱ����֤��AB+AD=CF��
��2����ͼ 2������ F ���߶� CA ��ʱ������ EA����֤��EA ƽ�֡�DEB��
��3����ͼ 3������ F ǡ��Ϊ�߶� CA ���е�ʱ��EF=1��������BDE �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A����1��0����B��3����1������PΪy����һ�㣬����ABP�����Ϊ3�������������ĵ�P����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��ͼ����A����2��6��������x���ཻ�ڵ�B��������������y=3x��ͼ���ཻ�ڵ�C����C�ĺ�����Ϊ1��
��1����k��b��ֵ��
��2������D��y�Ḻ�����ϣ�������S��COD=![]() S��BOC�����D�����꣮
S��BOC�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABD�ա�CDB����AB��CD�Ƕ�Ӧ�ߣ������ĸ������в���ȷ����( )

A. ��ABD�͡�CDB��������B. ��ABD�͡�CDB���ܳ����
C. ��A+��ABD=��C+��CBDD. AD��BC����AD=BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������ͼ1����֪![]() ��
��![]() ���ɵ�
���ɵ�![]() __________.
__________.

����ͼ2���ڢٵ������£����![]() ƽ��
ƽ��![]() ����
����![]() __________.
__________.

����ͼ3���ڢ١��ڵ������£����![]() ����
����![]() __________.
__________.

��2�����Խ���������⣺��֪��ͼ4��![]() ��
��![]() ��
��![]() ��
��![]() ��ƽ���ߣ�
��ƽ���ߣ�![]() ����
����![]() �Ķ���.
�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A����5��0����B��5��0����D��2��7��������AD����y���ڵ�C��
��1����C�������� ����
��2������P��B�������ÿ��1����λ���ٶ���BA�����˶���ͬʱ����Q��C�������Ҳ��ÿ��1����λ���ٶ���y�������᷽���˶�����P���˶���A��ʱ�����㶼ֹͣ�˶�������ӳ������˶���x�룮
�����ú�x�Ĵ���ʽ�ֱ��ʾP��Q��������ꣻ
����x��2ʱ��y�����Ƿ����һ��E��ʹ�á�AQE��������APQ�������ȣ������ڣ���E�����꣬�������ڣ�˵�����ɣ�
��3���ڣ�2���������£��ڵ�P��Q�˶������У�����Q��x���ƽ����OF����G��F�ֱ�λ��y����������ࣩ����GQP���APQ�Ľ�ƽ���߽��ڵ�M�����PMQ�Ĵ�С�����P��Q���˶����仯��������仯���������PMQ�Ķ������������仯����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com