
分析 (1)观察各式,即可得出规律:如果a、b是两个实数,则有a2+b2≥2ab;
(2)根据完全平方的计算结果是非负数证明即可;
(3)根据规律可得ab≤$\frac{1}{2}$(a2+b2).
解答 解:(1)规律是:如果a、b是两个实数,则有a2+b2≥2ab;
(2)∵(a-b)2≥0,
∴a2-2ab+b2≥0,
∴a2+b2≥2ab;
(3)∵a2+b2≥2ab,
∴ab≤$\frac{1}{2}$(a2+b2).
∵a+b=4,
∴b=4-a,
∴ab≤$\frac{1}{2}$[a2+(4-a)2]=a2-4a+8=(a-2)2+4≤4,
∴ab的最大值为4.
点评 此题主要考查了实数的大小的比较以及数字的变化规律,通过阅读题目,发现规律实质上是完全平方公式的变形:因为(a-b)2≥0,所以a2+b2≥2ab.


科目:初中数学 来源: 题型:选择题
| A. | x-1>y-1 | B. | $\frac{x}{3}$>$\frac{y}{3}$ | C. | x+1>y+1 | D. | -3x>-3y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
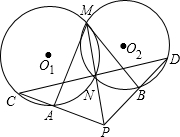 如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.
如图,已知⊙O1与⊙O2交于点M,N,MA是⊙O1的切线与⊙O2交于点A,MB是⊙O1的切线与⊙O2交于点B,延长线到点P,使MN=NP,PA与⊙O1交于点C,PB与⊙O2交于点D,求证:C、N、D三点共线,且CN=ND.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com