
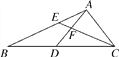
【题目】如图,在△ABC中,点D,E分别在边BC,AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF·EC.
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF·AD=AB·EF.
【答案】详见解析.
【解析】试题分析:(1)、根据已知条件的线段比值以及∠AEF=∠CEA得出△EAF和△ECA相似,从而得出∠EAF=∠ECA,根据AD=AC得出∠ADC=∠ACD,从而得出角度之间的关系;(2)、根据第一题中的相似得出∠EFA=∠CAB,根据BD=AD得出∠B=∠EAF,从而得出△FAE和△ABC相似,即![]() ,根据AC=AD得出结论.
,根据AC=AD得出结论.
试题解析:(1)∵AE2=EF·EC, ∴![]() =
=![]() , 又∵∠AEF=∠CEA, ∴△EAF∽△ECA,
, 又∵∠AEF=∠CEA, ∴△EAF∽△ECA,
∴∠EAF=∠ECA. ∵AD=AC, ∴∠ADC=∠ACD.
∵∠ACD=∠DCE+∠ECA=∠DCE+∠EAF, ∴∠ADC=∠DCE+∠EAF;
(2)由(1)可知△EAF∽△ECA, ∴∠EFA=∠EAC, 即∠EFA=∠CAB.
∵BD=AD, ∴∠B=∠BAD,即∠B=∠EAF, ∴△FAE∽△ABC,
∴![]() =
=![]() , ∴FA·AC=AB·FE, ∵AC=AD, ∴AF·AD=AB·EF.
, ∴FA·AC=AB·FE, ∵AC=AD, ∴AF·AD=AB·EF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N.
(1)求证:四边形CMAN是平行四边形.
(2)已知DE=2,FN=1,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一场暴雨过后,一洼地存雨水20米 3,如果将雨水全部排完需 t分钟,排水量为 a米 3/分,且排水时间为5~10分钟
(1)试写出 t与 a的函数关系式,并指出 a的取值范围;
(2)请画出函数图象
(3)根据图象回答:当排水量为3米 3/分时,排水的时间需要多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月23日是第23个“世界读书日”.某校围绕学生日人均阅读时间这一问题,对初二学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请你根据图中提供的信息解答下列问题:
(1)本次抽样调查的样本容量是 .
(2)请将条形统计图补充完整.
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角是 度.
(4)根据本次抽样调查,试估计我市12000名初二学生中日均阅读时间在0.5~1.5小时的有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,C为BD上一点,使得CA=CD,过点C作CE∥AD交AB于点E,过点D作DF⊥AD交AC的处长线于点F.
(1)若CD=3,求AF的长;
(2)若∠B=30°,∠ADC=40°,求证:AC=EC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com