
【题目】某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
(1)求甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式.
(2)求甲、乙第一次相遇的时间.
(3)直接写出乙回到侧门时,甲到侧门的路程.
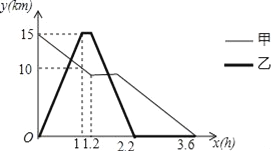
【答案】(1)y=﹣5x+15;(2)0.75h;(3)7km.
【解析】(1)根据函数图象可知点(0,15)和点(1,10)在甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数图象上,从而可以解答本题;
(2)根据函数图象可以分别求得甲乙刚开始两端对应的函数解析式,联立方程组即可求得第一次相遇的时间;
(3)根据函数图象可以得到在最后一段甲对应的函数解析式,乙到侧门时时间为2.2h,从而可以得到乙回到侧门时,甲到侧门的路程.
解:(1)设甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=kx+b,
∵点(0,15)和点(1,10)在此函数的图象上,
∴![]() ,
,
解得k=﹣5,b=15.
∴y=﹣5x+15.
即甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=﹣5x+15.
(2)设乙骑自行车从侧门匀速前往正门对应的函数关系式y=kx,
将(1,15)代入可得k=15,
∴乙骑自行车从侧门匀速前往正门对应的函数关系式y=15x,
∴![]() , 解得x=0.75.
, 解得x=0.75.
即第一次相遇时间为0.75h.
(3)乙回到侧门时,甲到侧门的路程是7km.
设甲休息了0.6小时后仍按原速继续行走对应的函数解析式为:y=kx+b.
将x=1.2代入y=﹣5x+15得,y=9.
∵点(1.8,9),(3.6,0)在y=kx+b上,
∴![]() ,
,
解得k=﹣5,b=18.
∴y=﹣5x+18.
将x=2.2代入y=﹣5x+18,得y=7.
即乙回到侧门时,甲到侧门的路程是7km.
“点睛”本题考查一次函数的应用,解题的关键是能看懂题意,根据数形结合的数学思想,找出所求问题需要的条件.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325 8430 8215 7453 7446 6754
7638 6834 7326 6830 8648 8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:

请根据以上信息解答下列问题:
(1)填空:![]() =__________,
=__________,![]() =__________;
=__________;
(2)补全频数统计图;
(3)这20名“健步走运动”团队成员一天步行步数的中位数落在_________组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
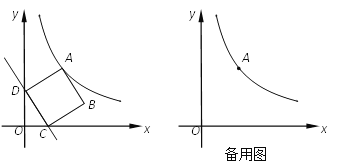
【题目】如图,在平面直角坐标系中,一次函数y=![]() x+4的图像与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=
x+4的图像与x轴、y轴分别相交于点C、D,四边形ABCD是正方形,反比例函数y=![]() 的图像在第一象限经过点A.
的图像在第一象限经过点A.
(1)求点A的坐标以及k的值:
(2)点P是反比例函数y=![]() (x>0)的图像上一点,且△PAO的面积为21,求点P的坐标.
(x>0)的图像上一点,且△PAO的面积为21,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装商贩同时卖出两套服装,每套均卖168元,其中一套盈利20%,另一套亏本20%,则这次交易中商贩( )
A. 不赔不赚 B. 赔14元 C. 赚14元 D. 赚37.2元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com