
������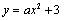 ��
�� ����A��B����
����A��B���� ����C����һ��ֱ����ͼ������ֱ������ϵ�У�ʹֱ�߱�
����C����һ��ֱ����ͼ������ֱ������ϵ�У�ʹֱ�߱� ��
��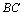 ��ֱ�߱�
��ֱ�߱�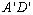 ��
��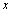 ����E����AC��F������������G��ֱ����һ��
����E����AC��F������������G��ֱ����һ��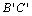 ��
��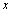 ����D������D���A�غ�ʱ����ֱ����
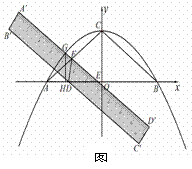
����D������D���A�غ�ʱ����ֱ����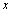 ������ƽ�ƣ�����E���B�غ�ʱ��ֹͣƽ�ƣ���ƽ�ƹ����У���FDE�������ֱ��ƽ�ƾ���ĺ���ͼ����ͼ��3����ʾ��
������ƽ�ƣ�����E���B�غ�ʱ��ֹͣƽ�ƣ���ƽ�ƹ����У���FDE�������ֱ��ƽ�ƾ���ĺ���ͼ����ͼ��3����ʾ��
��1���������DE�ij��������߽���ʽ��
��2����ֱ��ƽ�ƹ����У�ֱ�߱�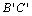 ���Ƿ����һ��P��ʹ��
���Ƿ����һ��P��ʹ��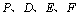 ���ɵ��ı��������Σ������ڣ����������P���ꣻ�������ڣ���˵�����ɣ�
���ɵ��ı��������Σ������ڣ����������P���ꣻ�������ڣ���˵�����ɣ�
��3����G��GH��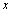 ����H
����H
�� ��ֱ��ƽ�ƹ����У��������GH+HO�����ֵ��
�ڵ�Q��R�ֱ���HC��HB���е㣬����ֱ��д����ֱ��ƽ�ƹ����У��߶�QRɨ����ͼ�ε�������ܳ���
����Ҫ����ѧ��һ�κ��������κ��������Ρ����������ε�֪ʶ���ۺ����ã������Ѷ�C��
 | |||
 |
�⣺��1�� C��0��3������OC=3
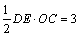 ��DE=2
��DE=2
��ͼ��1������FM��DE��M
 �� FM=
�� FM=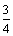
��������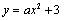 ����y��ԳƵ� AC=BC
����y��ԳƵ� AC=BC
���CBA=��CAB
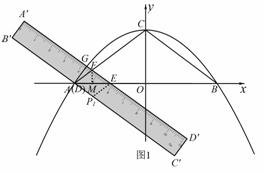 ��EF��BC
��EF��BC
���FED=��CBA
���FED=��FAE
��FA=FE
��FM��DE
��AM=ME=1
��FM��CO
���AFM�ס�ACO
��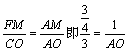
��AO=4 ����A��-4��0�� B��4��0��
��B��4��0������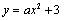 �ã�
�ã�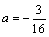 ��
�� ��������3��
��������3��
��2�� ����ͼ��1����D��A�غ�ʱ��FD=FE����E��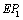 ��FA��B��C����
��FA��B��C����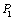 ��
��
���ı���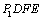 Ϊ���� ����ʱF(
Ϊ���� ����ʱF(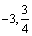 )
)
��F��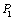 ����
����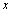 ��Գ� ��
��Գ� ��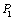 (
(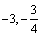 )
)
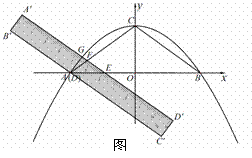
����ͼ��2����FE=ED=2ʱ����F�� ��ED��B��C����
��ED��B��C����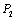 , ���ı���
, ���ı���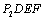 Ϊ����
����
�����ӳ� ��y����W����F��FN��x����N
��y����W����F��FN��x����N
��FE��BC ���FEN=��CBO
 ��
�� ��FEN=
��FEN= ��CBO=
��CBO=
��Rt��ENF�� ��FEN=
��FEN=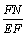 ��FN=
��FN=
ֱ��AC�Ľ���ʽΪ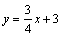 ,
,
��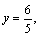 ��
��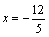

��FW=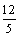 ��
��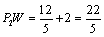
��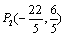
��3�� �� ��G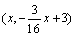
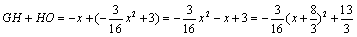
��GH+HO�����ֵΪ
�� ��ƽ�ƵĹ����У� QRʼ��ƽ���ҵ���BC��һ�룬����QRɨ����ͼ��Ϊƽ���ı���
��ͼ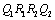
��HO=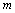 ����GH=
����GH=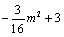
�ߡ�EFM�ס�EGH
��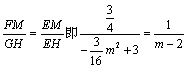
 ��
�� ����ȥ��
����ȥ��
����HO=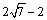
�� HB=HO+OB=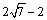 +4=
+4=
��
��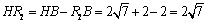
��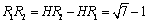
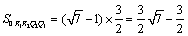
 ���ܳ�=
���ܳ�=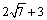


 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
һ�κ���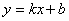 ���������ཻ��A��B���㣨A��x���ϣ����뷴��������
���������ཻ��A��B���㣨A��x���ϣ����뷴��������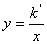 ��ͼ���ཻ��C�㣬��AO=2BO����C����Ϊ��-1,4��.
��ͼ���ཻ��C�㣬��AO=2BO����C����Ϊ��-1,4��.
��1����ȷ��һ�κ����뷴���������Ľ���ʽ��
��2����ʽ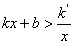 �Ľ⣻
�Ľ⣻
��3���ڽ��������У��㷢���õ�����Щ��ѧ˼�뷽�������д����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
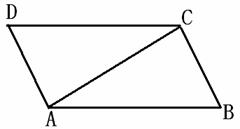
��ͼ��AC��ƽ���ı���ABCD�ĶԽ��ߣ�
��1���밴���²�����ͼ�������ͼ��������ͼ�ۼ�����
�ٷֱ���A��CΪԲ�ģ��Դ���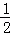 AC��Ϊ�뾶����������AC����Ľ���ֱ�ΪP��Q��
AC��Ϊ�뾶����������AC����Ľ���ֱ�ΪP��Q��
������PQ��PQ�ֱ���AB��AC��CD���ڵ�E��O��F��
��2����֤��AE=CF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
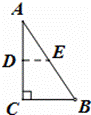
��ͼ��ֱ��������ֽƬABC�ġ�CΪ90�㣬��������ֽƬ����ͼʾ����λ��DE������Ȼ��Ѽ���������������ƴ�ӳɲ��ص���ͼ�Σ�����ѡ��������ƴ����ͼ���ǣ��� ����
A��ֱ������ B������ C���������� D��ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
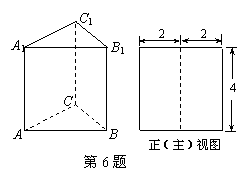
��ͼ�������� �IJ��ⳤ�͵���߳���Ϊ4���Ҳ���
�IJ��ⳤ�͵���߳���Ϊ4���Ҳ���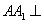 ����
����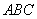 ��������������ͼ�DZ߳�Ϊ4�������Σ�����������ࣨ����ͼ�����Ϊ�� ��
��������������ͼ�DZ߳�Ϊ4�������Σ�����������ࣨ����ͼ�����Ϊ�� ��
A��4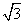 B��
B��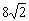 C��
C��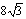 D��8
D��8
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com