
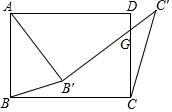
 如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则$\frac{CC'}{{{B}{B}'}}$=$\frac{\sqrt{74}}{5}$(结果保留根号).
如图,在矩形ABCD中,将∠ABC绕点A按逆时针方向旋转一定角度后,BC的对应边B'C'交CD边于点G.连接BB'、CC'.若AD=7,CG=4,AB'=B'G,则$\frac{CC'}{{{B}{B}'}}$=$\frac{\sqrt{74}}{5}$(结果保留根号). 分析 先连接AC,AG,AC',构造直角三角形以及相似三角形,根据△ABB'∽△ACC',可得到$\frac{CC′}{BB′}$=$\frac{AC}{AB}$,设AB=AB'=x,则AG=$\sqrt{2}$x,DG=x-4,Rt△ADG中,根据勾股定理可得方程72+(x-4)2=($\sqrt{2}$x)2,求得AB的长以及AC的长,即可得到所求的比值.
解答 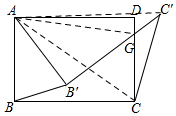 解:连接AC,AG,AC',
解:连接AC,AG,AC',
由旋转可得,AB=AB',AC=AC',∠BAB'=∠CAC',
∴$\frac{AB}{AC}$=$\frac{AB′}{AC′}$,
∴△ABB'∽△ACC',
∴$\frac{CC′}{BB′}$=$\frac{AC}{AB}$,
∵AB'=B'G,∠AB'G=∠ABC=90°,
∴△AB'G是等腰直角三角形,
∴AG=$\sqrt{2}$AB',
设AB=AB'=x,则AG=$\sqrt{2}$x,DG=x-4,
∵Rt△ADG中,AD2+DG2=AG2,
∴72+(x-4)2=($\sqrt{2}$x)2,
解得x1=5,x2=-13(舍去),
∴AB=5,
∴Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+{7}^{2}}$=$\sqrt{74}$,
∴$\frac{CC′}{BB′}$=$\frac{AC}{AB}$=$\frac{\sqrt{74}}{5}$,
故答案为:$\frac{\sqrt{74}}{5}$.
点评 本题主要考查了旋转的性质,相似三角形的判定与性质,等腰直角三角形的性质,解一元二次方程以及勾股定理的综合应用,解决问题的关键是作辅助线构造直角三角形以及相似三角形,依据相似三角形的对应边成比例,将$\frac{CC′}{BB′}$转化为$\frac{AC}{AB}$,并依据直角三角形的勾股定理列方程求解,从而得出矩形的宽AB,这也是本题的难点所在.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
 已知等腰△ABC的顶角∠A=36°(如图).
已知等腰△ABC的顶角∠A=36°(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
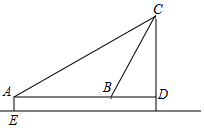 衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com