
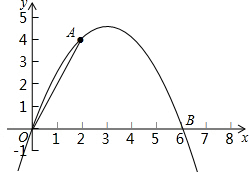
 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).分析 (1)把A与B坐标代入二次函数解析式求出a与b的值即可;
(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,分别表示出三角形OAD,三角形ACD,以及三角形BCD的面积,之和即为S,确定出S关于x的函数解析式,并求出x的范围,利用二次函数性质即可确定出S的最大值,以及此时x的值.
解答 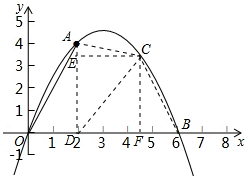 解:(1)将A(2,4)与B(6,0)代入y=ax2+bx,
解:(1)将A(2,4)与B(6,0)代入y=ax2+bx,
得$\left\{\begin{array}{l}{4a+2b=4}\\{36a+6b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=3}\end{array}\right.$;
(2)如图,过A作x轴的垂直,垂足为D(2,0),连接CD、CB,过C作CE⊥AD,CF⊥x轴,垂足分别为E,F,
S△OAD=$\frac{1}{2}$OD•AD=$\frac{1}{2}$×2×4=4;
S△ACD=$\frac{1}{2}$AD•CE=$\frac{1}{2}$×4×(x-2)=2x-4;
S△BCD=$\frac{1}{2}$BD•CF=$\frac{1}{2}$×4×(-$\frac{1}{2}$x2+3x)=-x2+6x,
则S=S△OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x,
∴S关于x的函数表达式为S=-x2+8x(2<x<6),
∵S=-x2+8x=-(x-4)2+16,
∴当x=4时,四边形OACB的面积S有最大值,最大值为16.
点评 此题考查了待定系数法求二次函数解析式,以及二次函数的最值,熟练掌握二次函数的性质是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
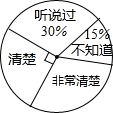 第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{400}{x}$=$\frac{400+100}{x+20}$ | B. | $\frac{400}{x}$=$\frac{400-100}{x-20}$ | ||
| C. | $\frac{400}{x}$=$\frac{400+100}{x-20}$ | D. | $\frac{400}{x}$=$\frac{400-100}{x+20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 1 | 5 | 4 | 2 |
| A. | 众数是14 | B. | 极差是3 | C. | 中位数是14.5 | D. | 平均数是14.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com