
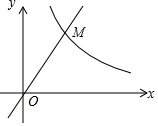
 如图,点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,OM=4,则k的值为4$\sqrt{3}$.
如图,点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,OM=4,则k的值为4$\sqrt{3}$. 分析 作MN⊥x轴于N,得出M(x,$\sqrt{3}$x),在Rt△OMN中,由勾股定理得出方程,解方程求出x=2,得出M(2,2$\sqrt{3}$),即可求出k的值.
解答 解:作MN⊥x轴于N,如图所示:
设M(x,y),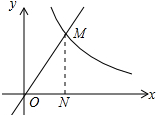
∵点M是函数y=$\sqrt{3}$x与y=$\frac{k}{x}$的图象在第一象限内的交点,
∴M(x,$\sqrt{3}$x),
在Rt△OMN中,由勾股定理得:x2+($\sqrt{3}$x)2=42,
解得:x=2,
∴M(2,2$\sqrt{3}$),
代入y=$\frac{k}{x}$得:k=2×2$\sqrt{3}$=4$\sqrt{3}$;
故答案为:4$\sqrt{3}$.
点评 本题考查了反比例函数与一次函数的图象得交点、勾股定理、反比例函数解析式的求法;求出点M的坐标是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
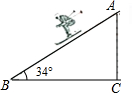 如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了280米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了280米.(参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
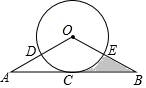 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,$\widehat{CD}$=$\widehat{CE}$
如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,$\widehat{CD}$=$\widehat{CE}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数不变,方差不变 | B. | 平均数不变,方差变大 | ||
| C. | 平均数不变,方差变小 | D. | 平均数变小,方差不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com