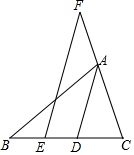
如图.在△ABC中.∠B=40°.∠C=70°.AD是△ABC的角平分线.点E在BD上.点F在CA的延长线上.EF∥AD．(1)求∠BAF的度数．(2)求∠F的度数．题目和参考答案——青夏教育精英家教网—

1．

如图，在△ABC中，∠B=40°，∠C=70°，AD是△ABC的角平分线，点E在BD上，点F在CA的延长线上，EF∥AD．
（1）求∠BAF的度数．
（2）求∠F的度数．

分析（1）根据外角的性质即可得到结论；
（2）根据角平分线的定义得到∠DAC=$\frac{1}{2}$BAC=35°，根据平行线的性质即可得到结论．

解答解：（1）∵∠BAF=∠B+∠C，
∵∠B=40°，∠C=70°，
∴∠BAF=110°；
（2）∵∠BAF=110°，
∴∠BAC=70°，
∵AD是△ABC的角平分线，
∴∠DAC=$\frac{1}{2}$BAC=35°，
∵EF∥AD，
∴∠F=∠DAC=35°．

点评本题考查了三角形外角的性质，平行线的性质，三角形的内角和，角平分线的定义，熟练掌握三角形外角的性质是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

18．

如图，一个大圆和四个面积相等的小圆，已知大圆半径等于小圆直径，小圆半径为a厘米，那么阴影部分的面积为πa²平方厘米．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

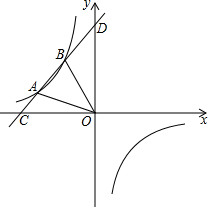如图，直线y=mx+n（m≠0）与双曲线y=$\frac{k}{x}$（k≠0）交于A、B两点，直线AB与坐标轴分别交于C、D两点，连接OA，若OA=2$\sqrt{10}$，tan∠AOC=$\frac{1}{3}$，点B（-3，b）．
（1）分别求出直线AB与双曲线的解析式；
（2）连接OB，求S_△AOB．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．

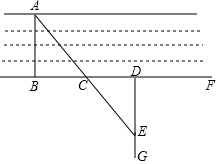小明家门前有一条小河，村里准备在河面上架上一座桥，但河宽AB无法直接测量，爱动脑的小明想到了如下方法：在与AB垂直的岸边BF上取两点C、D使CD=CB，再引出BF的垂线DG，在DG上取一点E，并使A、C、E在一条直线上，这时测出线段DE的长度就是AB的长．
（1）按小明的想法填写题目中的空格；
（2）请完成推理过程．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．（1）计算：$\sqrt{3}$（$\sqrt{2}$+$\sqrt{3}$）-$\sqrt{24}$
（2）解方程：x²-2x=4．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

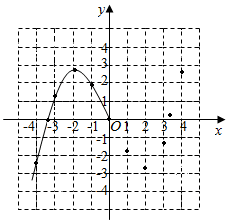某学习小组在研究函数y=$\frac{1}{6}$x³-2x的图象与性质时，已列表、描点并画出了图象的一部分．

x	…	-4	-3.5	-3	-2	-1	0	1	2	3	3.5	4	…
y	…	-$\frac{8}{3}$	-$\frac{7}{48}$	$\frac{3}{2}$	$\frac{8}{3}$	$\frac{11}{6}$	0	-$\frac{11}{6}$	-$\frac{8}{3}$	-$\frac{3}{2}$	$\frac{7}{48}$	$\frac{8}{3}$	…

（1）请补全函数图象；
（2）方程$\frac{1}{6}$x³-2x=-2实数根的个数为3；
（3）观察图象，写出该函数的两条性质．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．“一带一路”的战略构想为国内许多企业的发展带来了新的机遇，某公司生产A，B两种机械设备，每台B种设备的成本是A种设备的1.5倍，公司若投入16万元生产A种设备，36万元生产B种设备，则可生产两种设备共10台．请解答下列问题：
（1）A、B两种设备每台的成本分别是多少万元？
（2）若A，B两种设备每台的售价分别是6万元，10万元，公司决定生产两种设备共60台，计划销售后获利不低于126万元，且A种设备至少生产53台，求该公司有几种生产方案；
（3）在（2）的条件下，销售前公司决定从这批设备中拿出一部分，赠送给“一带一路”沿线的甲国，剩余设备全部售出，公司仍获利44万元，赠送的设备采用水路运输和航空运输两种方式，共运输4次，水路运输每次运4台A种设备，航空运输每次运2台B种设备（运输过程中产生的费用由甲国承担）．直接写出水路运输的次数．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．