
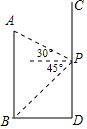
 如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.
如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.分析 (1)点P作AB 的垂线,垂足为E,根据题意可得出四边形PDBE是矩形,再由∠EPB=45°可知BE=PE=36m,故可得出PD的长;
(2)AE=PE•tan30°得出AE的长,进而可得出结论.
解答 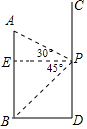 解:(1)如图,过点P作AB 的垂线,垂足为E,
解:(1)如图,过点P作AB 的垂线,垂足为E,
∵PD⊥AB,DB⊥AB,
∴四边形PDBE是矩形,
∵BD=36m,∠EPB=45°,
∴BE=PE=36m,
∴PD=BE=36m.
(2)∵AE=PE•tan30°=36×$\frac{\sqrt{3}}{3}$=12$\sqrt{3}$(m),
∴AB=AE+BE=(12$\sqrt{3}$+36)m.
答:建筑物AB的高为$\sqrt{3}$米.
(1)PD的高为36米
(2)大楼AB的高为($12\sqrt{3}+36$)米
点评 本题考查的是解直角三角形的应用,仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
 甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:
甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
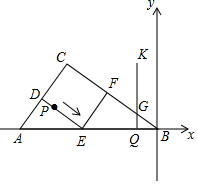 如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.以AB所在直线为x轴,B点为坐标原点建立平面直角坐标系,点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长度的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长度的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G,点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.以AB所在直线为x轴,B点为坐标原点建立平面直角坐标系,点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长度的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长度的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G,点P,Q同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
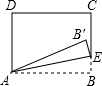 如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.
如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
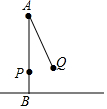 如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)
如图,旗杆AB顶端系一根绳子AP,绳子底端离地面的距离为1m,小明将绳子拉到AQ的位置,测得∠PAQ=25°,此时点Q离地面的高度为1.5m,求旗杆的高度(结果保留整数.sin25°=0.42,cos25°=0.90,tan25°=0.47)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com