【题目】如图，△ABC中，∠BAC=90°，AB=AC, D是△ABC内一点，∠DAC=∠DCA=15°，则∠BDA=______.
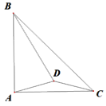
【答案】75°
【解析】
以AD为边，在△ADB中作等边三角形ADE，连接BE．可证得△EAB≌△DAC，再证△BEA≌△BED，得到BA=BD，利用等边对等角即可得结论．
如图，以AD为边，在△ADB中作等边三角形ADE，连接BE.
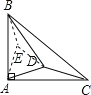
∵∠BAE=90°-60°-15°=15°，
∴∠BAE=∠CAD=15°，
在△EAB和△DAC中，
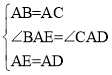
∴△EAB≌△DAC(SAS)，
∴∠BEA=∠CDA=180°-15°-15°=150°，
∴∠BED=360°-∠BEA-60°=150°，即∠BEA=∠BED；
在△BEA和△BED中，
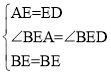
∴△BEA≌△BED(SAS)，
∴BA=BD.
∴∠BDA=∠BAD=90°-∠DAC=75°
故答案为：75°.
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y1=x2-2x-3与x轴相交于点A，B(点A在B的左侧)，与y轴相交于点C，直线y2=kx+b经过点B，C．
（1）求直线BC的函数关系式；
（2）当y1>y2时，请直接写出x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中
，
，詹姆斯在探究筝形的性质时，得到如下结论：
；
；
≌
；
四边形ABCD的面积
其中正确的结论有
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】贵州省是我国首个大数据综合试验区，大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值，为创建大数据应用示范城市，我市某机构针对市民最关心的四类生活信息进行了民意调查（被调查者每人限选一项），下面是部分四类生活信息关注度统计图表，请根据图中提供的信息解答下列问题：
（1）本次参与调查的人数有 人；
（2）关注城市医疗信息的有 人，并补全条形统计图；
（3）扇形统计图中，D部分的圆心角是 度；
（4）说一条你从统计图中获取的信息．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是等边△ABC内部一点，∠APB，∠BPC，∠CPA的大小之比是5：6：7，则以PA、PB、PC为边的三角形的三个内角的大小之比是（从小到大）（ ）
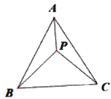
A.2：3：4B.4：5：6C.3：4：5D.不确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知⊙O的半径为2，弦BC的长为
，点A为弦BC所对优弧上任意一点（B，C两点除外）.
（1）求∠BAC的度数；
（2）求△ABC面积的最大值.
（参考数据：
，
，
.）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，A(-a,0),B(b,0),C(0,c),且满足
.
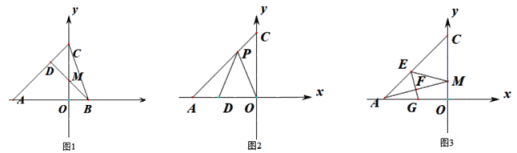
(1)如图1，过B作BD⊥AC,交y轴于M，垂足为D，求M点的坐标．
(2)如图2，若a=3
，AC=6，点P为线段AC上一点，D为x轴负半轴上一点，且PD=PO，∠DPO=45°，求点D的坐标．
(3)如图3，M在OC上，E在AC上，满足∠CME=∠OMA,EF⊥AM交AO于G，垂足为F，试猜想线段OG,OM,CM三者之间的数量关系，并给出证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用适当的方法解下列方程．
（1）x2﹣x﹣1=0；
（2）x2﹣2x=2x+1；
（3）x（x﹣2）﹣3x2=﹣1；
（4）（x+3）2=（1﹣2x）2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知A，B，C，D为矩形的四个顶点，AB＝16 cm，AD＝6 cm，动点P，Q分别从点A，C同时出发，点P以3 cm/s的速度向点B移动，一直到点B为止，点Q以2 cm/s的速度向点D移动，当点P停止运动时，点Q也停止运动．问：
(1)P，Q两点从开始出发多长时间时，四边形PBCQ的面积是33 cm2?
(2)P，Q两点从开始出发多长时间时，点P与点Q之间的距离是10 cm?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com