
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßC£ŗy=ax2+bx+cÓėxÖįĻą½»ÓŚA£¬BĮ½µć£¬¶„µćĪŖD£Ø0£¬4£©£¬AB=4 ![]() £¬ÉčµćF£Øm£¬0£©ŹĒxÖįµÄÕż°ėÖįÉĻŅ»µć£¬½«Å×ĪļĻßCČʵćFŠż×Ŗ180”ć£¬µĆµ½ŠĀµÄÅ×ĪļĻßC”䣮
£¬ÉčµćF£Øm£¬0£©ŹĒxÖįµÄÕż°ėÖįÉĻŅ»µć£¬½«Å×ĪļĻßCČʵćFŠż×Ŗ180”ć£¬µĆµ½ŠĀµÄÅ×ĪļĻßC”䣮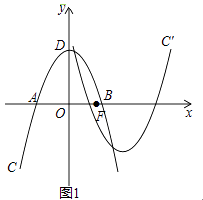
£Ø1£©ĒóÅ×ĪļĻßCµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōÅ×ĪļĻßC”äÓėÅ×ĪļĻßCŌŚyÖįµÄÓŅ²ąÓŠĮ½øö²»Ķ¬µÄ¹«¹²µć£¬ĒómµÄȔֵ·¶Ī§£®
£Ø3£©ČēĶ¼2£¬PŹĒµŚŅ»ĻóĻŽÄŚÅ×ĪļĻßCÉĻŅ»µć£¬Ėüµ½Į½×ų±źÖįµÄ¾ąĄėĻąµČ£¬µćPŌŚÅ×ĪļĻßC”äÉĻµÄ¶ŌÓ¦µćP”䣬ÉčMŹĒCÉĻµÄ¶Æµć£¬NŹĒC”äÉĻµÄ¶Æµć£¬ŹŌĢ½¾æĖıߊĪPMP”äNÄÜ·ń³ÉĪŖÕż·½ŠĪ£æČōÄÜ£¬Ēó³ömµÄÖµ£»Čō²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ£®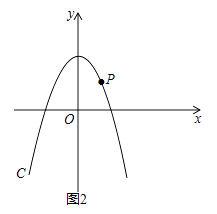
”¾“š°ø”æ
£Ø1£©
½ā£ŗÓÉĢāŅāÅ×ĪļĻߵĶ„µćC£Ø0£¬4£©£¬A£Ø2 ![]() £¬0£©£¬ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+4£¬
£¬0£©£¬ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+4£¬
°ŃA£Ø2 ![]() £¬0£©“śČėæɵĆa=©
£¬0£©“śČėæɵĆa=© ![]() £¬
£¬
”ąÅ×ĪļĻßCµÄŗÆŹż±ķ“ļŹ½ĪŖy=© ![]() x2+4
x2+4
£Ø2£©
½ā£ŗÓÉĢāŅāÅ×ĪļĻßC”äµÄ¶„µć×ų±źĪŖ£Ø2m£¬©4£©£¬ÉčÅ×ĪļĻßC”äµÄ½āĪöŹ½ĪŖy= ![]() £Øx©m£©2©4£¬
£Øx©m£©2©4£¬
ÓÉ  £¬ĻūČ„yµĆµ½x2©2mx+2m2©8=0£¬
£¬ĻūČ„yµĆµ½x2©2mx+2m2©8=0£¬
ÓÉĢāŅā£¬Å×ĪļĻßC”äÓėÅ×ĪļĻßCŌŚyÖįµÄÓŅ²ąÓŠĮ½øö²»Ķ¬µÄ¹«¹²µć£¬
ŌņÓŠ  £¬½āµĆ2£¼m£¼2
£¬½āµĆ2£¼m£¼2 ![]() £¬
£¬
”ąĀś×ćĢõ¼žµÄmµÄȔֵ·¶Ī§ĪŖ2£¼m£¼2 ![]()
£Ø3£©
½ā£ŗ½įĀŪ£ŗĖıߊĪPMP”äNÄܳÉĪŖÕż·½ŠĪ£®
ĄķÓÉ£ŗ1ĒéŠĪ1£¬ČēĶ¼£¬×÷PE”ĶxÖįÓŚE£¬MH”ĶxÖįÓŚH£®

ÓÉĢāŅāŅ×ÖŖP£Ø2£¬2£©£¬µ±”÷PFMŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£¬
”ąPF=FM£¬”ĻPFM=90”ć£¬
Ņ×Ö¤”÷PFE”Õ”÷FMH£¬æɵĆPE=FH=2£¬EF=HM=2©m£¬
”ąM£Øm+2£¬m©2£©£¬
”ßµćMŌŚy=© ![]() x2+4ÉĻ£¬
x2+4ÉĻ£¬
”ąm©2=© ![]() £Øm+2£©2+4£¬½āµĆm=
£Øm+2£©2+4£¬½āµĆm= ![]() ©3»ņ©
©3»ņ© ![]() ©3£ØÉįĘś£©£¬
©3£ØÉįĘś£©£¬
”ąm= ![]() ©3Ź±£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£®
©3Ź±£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£®
ĒéŠĪ2£¬ČēĶ¼£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£¬Ķ¬·ØæɵĆM£Øm©2£¬2©m£©£¬

°ŃM£Øm©2£¬2©m£©“śČėy=© ![]() x2+4ÖŠ£¬2©m=©
x2+4ÖŠ£¬2©m=© ![]() £Øm©2£©2+4£¬½āµĆm=6»ņ0£ØÉįĘś£©£¬
£Øm©2£©2+4£¬½āµĆm=6»ņ0£ØÉįĘś£©£¬
”ąm=6Ź±£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ
”¾½āĪö”æ£Ø1£©ÓÉĢāŅāÅ×ĪļĻߵĶ„µćC£Ø0£¬4£©£¬A£Ø2 ![]() £¬0£©£¬ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+4£¬°ŃA£Ø2
£¬0£©£¬ÉčÅ×ĪļĻߵĽāĪöŹ½ĪŖy=ax2+4£¬°ŃA£Ø2 ![]() £¬0£©“śČėæɵĆa=©
£¬0£©“śČėæɵĆa=© ![]() £¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£»£Ø2£©ÓÉĢāŅāÅ×ĪļĻßC”äµÄ¶„µć×ų±źĪŖ£Ø2m£¬©4£©£¬ÉčÅ×ĪļĻßC”äµÄ½āĪöŹ½ĪŖy=
£¬ÓÉ“Ė¼“æɽā¾öĪŹĢā£»£Ø2£©ÓÉĢāŅāÅ×ĪļĻßC”äµÄ¶„µć×ų±źĪŖ£Ø2m£¬©4£©£¬ÉčÅ×ĪļĻßC”äµÄ½āĪöŹ½ĪŖy= ![]() £Øx©m£©2©4£¬ÓÉ
£Øx©m£©2©4£¬ÓÉ  £¬ĻūČ„yµĆµ½x2©2mx+2m2©8=0£¬ÓÉĢāŅā£¬Å×ĪļĻßC”äÓėÅ×ĪļĻßCŌŚyÖįµÄÓŅ²ąÓŠĮ½øö²»Ķ¬µÄ¹«¹²µć£¬ŌņÓŠ
£¬ĻūČ„yµĆµ½x2©2mx+2m2©8=0£¬ÓÉĢāŅā£¬Å×ĪļĻßC”äÓėÅ×ĪļĻßCŌŚyÖįµÄÓŅ²ąÓŠĮ½øö²»Ķ¬µÄ¹«¹²µć£¬ŌņÓŠ  £¬½ā²»µČŹ½×鼓æɽā¾öĪŹĢā£»£Ø3£©ĒéŠĪ1£¬ĖıߊĪPMP”äNÄܳÉĪŖÕż·½ŠĪ£®×÷PE”ĶxÖįÓŚE£¬MH”ĶxÖįÓŚH£®ÓÉĢāŅāŅ×ÖŖP£Ø2£¬2£©£¬µ±”÷PFMŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£¬ĶĘ³öPF=FM£¬”ĻPFM=90”ć£¬Ņ×Ö¤”÷PFE”Õ”÷FMH£¬æɵĆPE=FH=2£¬EF=HM=2©m£¬æɵĆM£Øm+2£¬m©2£©£¬ĄķÓÉ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£»ĒéŠĪ2£¬ČēĶ¼£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£¬Ķ¬·ØæɵĆM£Øm©2£¬2©m£©£¬ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£®
£¬½ā²»µČŹ½×鼓æɽā¾öĪŹĢā£»£Ø3£©ĒéŠĪ1£¬ĖıߊĪPMP”äNÄܳÉĪŖÕż·½ŠĪ£®×÷PE”ĶxÖįÓŚE£¬MH”ĶxÖįÓŚH£®ÓÉĢāŅāŅ×ÖŖP£Ø2£¬2£©£¬µ±”÷PFMŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£¬ĶĘ³öPF=FM£¬”ĻPFM=90”ć£¬Ņ×Ö¤”÷PFE”Õ”÷FMH£¬æɵĆPE=FH=2£¬EF=HM=2©m£¬æɵĆM£Øm+2£¬m©2£©£¬ĄķÓÉ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£»ĒéŠĪ2£¬ČēĶ¼£¬ĖıߊĪPMP”äNŹĒÕż·½ŠĪ£¬Ķ¬·ØæɵĆM£Øm©2£¬2©m£©£¬ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£®
”¾æ¼µć¾«Īö”æøł¾ŻĢāÄæµÄŅŃÖŖĢõ¼ž£¬ĄūÓƶž“ĪŗÆŹżµÄĶ¼ĻóŗĶ¶ž“ĪŗÆŹżµÄŠŌÖŹµÄĻą¹ŲÖŖŹ¶æÉŅŌµĆµ½ĪŹĢāµÄ“š°ø£¬ŠčŅŖÕĘĪÕ¶ž“ĪŗÆŹżĶ¼Ļń¹Ų¼üµć£ŗ1”¢æŖæŚ·½Ļņ2”¢¶Ō³ĘÖį 3”¢¶„µć 4”¢ÓėxÖį½»µć 5”¢ÓėyÖį½»µć£»Ōö¼õŠŌ£ŗµ±a>0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ų¼õŠ”£»¶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ųŌö“ó£»µ±a<0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ųŌö“󣻶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ų¼õŠ”£®


 æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø
æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø æĪŹ±ÕĘæŲĖęĢĆĮ·Ļ°ĻµĮŠ“š°ø
æĪŹ±ÕĘæŲĖęĢĆĮ·Ļ°ĻµĮŠ“š°ø Ņ»æĪŅ»Į·Ņ»±¾ĶØĻµĮŠ“š°ø
Ņ»æĪŅ»Į·Ņ»±¾ĶØĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ°ĖÄź¼¶£Ø1£©°ąŃŠ¾æŠŌѧĻ°Š”×éĪŖŃŠ¾æČ«Š£Ķ¬Ń§æĪĶāŌĶĮĒéæö£¬ŌŚČ«Š£Ė껜ŃūĒėĮĖ²æ·ÖĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£¬Ķ³¼ĘĶ¬Ń§ĆĒŅ»øöŌĀŌĶĮæĪĶāŹéµÄŹżĮ棬²¢»ęÖĘĮĖŅŌĻĀĶ³¼ĘĶ¼£®

Ēėøł¾ŻĶ¼ÖŠŠÅĻ¢½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©¹²ÓŠ¶ąÉŁĆūĶ¬Ń§²ĪÓėĪŹ¾ķµ÷²é£»
£Ø2£©²¹Č«ĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£»
£Ø3£©Č«Š£¹²ÓŠŃ§Éś1500ČĖ£¬Ēė¹Ą¼ĘøĆŠ£Ń§ÉśŅ»øöŌĀŌĶĮ2±¾æĪĶāŹéµÄČĖŹżŌ¼ĪŖ¶ąÉŁ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø2015¹šĮÖ£©”°Č«ĆńŌĶĮ”±ÉīČėČĖŠÄ£¬ŗƶĮŹé£¬¶ĮŗĆŹé£¬ČĆČĖÖÕÉķŹÜŅę£®ĪŖĀś×ćĶ¬Ń§ĆĒµÄ¶ĮŹéŠčĒó£¬Ń§Š£Ķ¼Źé¹Ż×¼±øµ½ŠĀ»ŖŹéµź²É¹ŗĪÄѧĆūÖųŗĶ¶ÆĀžŹéĮ½ĄąĶ¼Źé£®¾ĮĖ½ā£¬20±¾ĪÄѧĆūÖųŗĶ40±¾¶ÆĀžŹé¹²Šč1520ŌŖ£¬20±¾ĪÄѧĆūÖų±Č20±¾¶ÆĀžŹé¶ą440ŌŖ£Ø×¢£ŗĖł²É¹ŗµÄĪÄѧĆūÖų¼Ūøń¶¼Ņ»Ńł£¬Ėł²É¹ŗµÄ¶ÆĀžŹé¼Ūøń¶¼Ņ»Ńł£©£®
£Ø1£©ĒóĆæ±¾ĪÄѧĆūÖųŗĶ¶ÆĀžŹéø÷¶ąÉŁŌŖ£æ
£Ø2£©ČōѧŠ£ŅŖĒó¹ŗĀņ¶ÆĀžŹé±ČĪÄѧĆūÖų¶ą20±¾£¬¶ÆĀžŹéŗĶĪÄѧĆūÖų×ÜŹż²»µĶÓŚ72±¾£¬×Ü·ŃÓĆ²»³¬¹ż2000ŌŖ£¬ĒėĒó³öĖłÓŠ·ūŗĻĢõ¼žµÄ¹ŗŹé·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
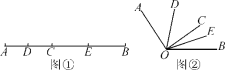
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŅŃÖŖĻ߶ĪAB£½16 cm£¬µćCĪŖĻ߶ĪABÉĻµÄŅ»øö¶Æµć(µćC²»ÓėA£¬BÖŲŗĻ)£¬µćD£¬E·Ö±šŹĒACŗĶBCµÄÖŠµć£®
(1)ĒóDEµÄ³¤£»
(2)ÖŖŹ¶ĒØŅĘ£ŗČēĶ¼¢Ś£¬ŅŃÖŖ”ĻAOB£½130”ć£¬¹ż½ĒµÄÄŚ²æČĪŅ»µćC»ÉäĻßOC£¬ČōOD£¬OE·Ö±šĘ½·Ö”ĻAOCŗĶ”ĻBOC£¬ŹŌĖµĆ÷”ĻDOEµÄ“óŠ”ÓėÉäĻßOCµÄĪ»ÖĆĪŽ¹Ų£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ĻČ»Æ¼ņ£¬ŌŁĒóÖµ£ŗ 2(m2 mn 1) 3(![]() m2 2mn 4) £¬ĘäÖŠ m
m2 2mn 4) £¬ĘäÖŠ m ![]() £¬n 3 £®
£¬n 3 £®
£Ø2£©ŅŃÖŖ 2a b 5 0 £¬ĒóÕūŹ½ 6a b Óė 2a 3b 27 µÄŗĶµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ
£Ø1£©¼ĘĖć£ŗ| ![]() ©1|©
©1|© ![]() +2sin45”ć+£Ø
+2sin45”ć+£Ø ![]() £©©2£»
£©©2£»
£Ø2£©½ā²»µČŹ½×é£ŗ  £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
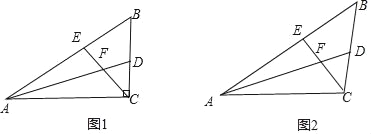
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ”÷ABCÖŠ£¬”ĻACBŹĒÖ±½Ē£¬”ĻB£½60”ć£¬AD”¢CE·Ö±šŹĒ”ĻBAC”¢”ĻBCAµÄĘ½·ÖĻߣ¬AD”¢CEĻą½»ÓŚµćF£®
(1)Ö±½ÓŠ“³ö”ĻAFCµÄ¶ČŹż£ŗ”” ””£»
(2)ĒėÄćÅŠ¶Ļ²¢Š“³öFEÓėFDÖ®¼äµÄŹżĮæ¹ŲĻµ£»
(3)ČēĶ¼2£¬ŌŚ”÷ABCÖŠ£¬Čē¹ū”ĻACB²»ŹĒÖ±½Ē£¬¶ų(1)ÖŠµÄĘäĖüĢõ¼ž²»±ä£¬ŹŌÅŠ¶ĻĻ߶ĪAE”¢CDÓėACÖ®¼äµÄŹżĮæ¹ŲĻµ²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬A”¢D”¢F”¢BŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬AD£½BF£¬AE£½BC£¬ĒŅAE”ĪBC£®
ĒóÖ¤£ŗ£Ø1£©EF£½CD£»£Ø2£©EF”ĪCD£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
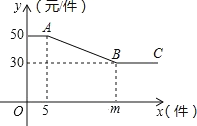
”¾ĢāÄæ”æijÉĢµź¾ĻśÄ³ÖÖĶę¾ß£¬øĆĶę¾ßĆæøö½ų¼Ū 20 ŌŖ£¬ĪŖ½ųŠŠ“ŁĻś£¬ÉĢµźÖʶØČēĻĀ”°ÓÅ»Ż”± ·½°ø£ŗČē¹ūŅ»“ĪĻśŹŪŹżĮæ²»³¬¹ż 5 øö£¬ŌņĆæøö°“ 50 ŌŖĻśŹŪ£ŗČē¹ūŅ»“ĪĻśŹŪŹżĮ泬¹ż 5 øö£¬ŌņĆæŌö¼ÓŅ»øö£¬ĖłÓŠĶę¾ß¾ł½µµĶ 1 ŌŖĻśŹŪ£¬µ«µ„¼Ū²»µĆµĶÓŚ 30 ŌŖ£¬Ņ»“ĪĻśŹŪøĆĶę¾ßµÄµ„¼Ū y£ØŌŖ£©ÓėĻśŹŪŹżĮæ x£Øøö£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĻĀĶ¼ĖłŹ¾£®
£Ø1£©½įŗĻĶ¼ŠĪ£¬Ēó³ö m µÄÖµ£»ÉäĻß BC Ėł±ķŹ¾µÄŹµ¼ŹŅāŅåŹĒŹ²Ć“£»
£Ø2£©ĒóĻ߶Ī AB Āś×ćµÄ y Óė x Ö®¼äµÄŗÆŹż½āĪöŹ½£¬²¢Ö±½ÓŠ“³ö×Ō±äĮæµÄȔֵ·¶Ī§£»
£Ø3£©µ±ĻśŹŪ 15 øöŹ±£¬ÉĢµźµÄĄūČóŹĒ¶ąÉŁŌŖ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com