
【题目】已知:如图,点E、F分别是AB和CD上的点,DE、AF分别交BC于G、H,∠A=∠D,∠1=∠2,试说明∠B=∠C.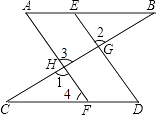
阅读下面的解题过程,在横线上补全推理过程或依据.
解:∵∠1=∠2(已知)
∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换)
∴AF∥DE( )
∴∠4=∠D( )
又∵∠A=∠D(已知)
∴∠4=∠A( )
∴ ( )
∴∠B=∠C( )
【答案】解:∵∠1=∠2(已知),
∠1=∠3(对顶角相等),
∴∠2=∠3(等量代换),
∴AF∥DE(同位角相等,两直线平行),
∴∠4=∠D(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴∠4=∠A(等量代换),
∴AB∥CD(内错角相等,两直线平行),
∴∠B=∠C(两直线平行,内错角相等).
【解析】根据平行线的性质和判断方法,两直线平行,同位角、内错角相等;同位角、内错角相等,两直线平行.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】设点A(m,n)在x轴上,且位于原点的左侧,则下列结论正确的是( )
A. m=0,n为一切数 B. m=0,n<0
C. m为一切数,n=0 D. m<0,n=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 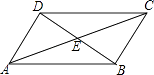
A.6
B.12
C.20
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则 秒时四边形ADFE是平行四边形.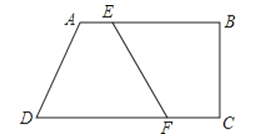
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,1),N(2,0),△MNP和△M1N1P1的顶点都在格点上,△MNP与△M1N1P1是关于某一点中心对称,则对称中心的坐标为 .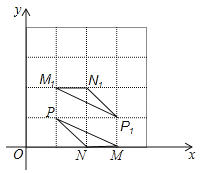
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com