
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图中全等的三角形只有两对;②△ABC的面积等于四边形CDOE面积的2倍;③OD=OE;④CE+CD=BC,其中正确的结论有( )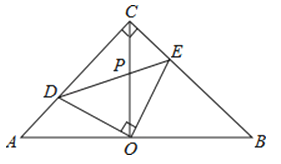
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:结论①错误.理由如下:
图中全等的三角形有3对,分别为△AOC≌△BOC,△AOD≌△COE,△COD≌△BOE.
由等腰直角三角形的性质,可知OA=OC=OB,易得△AOC≌△BOC.
∵OC⊥AB,OD⊥OE,
∴∠AOD=∠COE.
在△AOD与△COE中, ,
,
∴△AOD≌△COE(ASA).
同理可证:△COD≌△BOE.
结论②正确.理由如下:
∵△AOD≌△COE,
∴S△AOD=S△COE ,
∴S四边形CDOE=S△COD+S△COE=S△COD+S△AOD=S△AOC=![]() S△ABC ,
S△ABC ,
即△ABC的面积等于四边形CDOE的面积的2倍.
结论③正确,理由如下:∵△AOD≌△COE,
∴OD=OE;
结论④正确,理由如下:
∵△AOD≌△COE,
∴CE=AD,
∵AB=AC,
∴CD=EB,
∴CD+CE=EB+CE=BC.
综上所述,正确的结论有3个.
故选:C.
结论①错误.因为图中全等的三角形有3对;
结论②正确.由全等三角形的性质可以判断;
结论③正确.利用全等三角形的性质可以判断.
结论④正确.利用全等三角形和等腰直角三角形的性质可以判断.


科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,以△ABC 的一边为边画等腰三角形,使得它的第三个顶点在△ABC 的其他边上,试画出所有不同的等腰三角形并说明画图方法.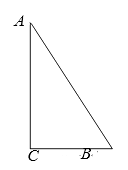
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校国旗护卫队成员的身高分布如下表:
身高/cm | 159 | 160 | 161 | 162 |
人数 | 7 | 10 | 9 | 9 |
则学校国旗护卫队成员的身高的众数和中位数分别是( )
A.160和160
B.160和160.5
C.160和161
D.161和161
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中属于不确定事件的是( )
A.抛出的篮球会落下B.从装有黑球,白球的袋里摸出红球
C.367人中至少有2人是同月同日出生D.买1张彩票,中500万大奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合采用抽样调查的是( )
A.检查一枚用于发射卫星的运载火箭的各零部件
B.了解全班同学身高状况
C.检查一批灯泡的使用寿命
D.奥运会上对参赛运动员进行的尿样检查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A、篮球,B、乒乓球,C、羽毛球,D、足球.为了解学生最喜欢哪一种活动项目,随机从2400名学生中抽取部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有人;
(2)请你将条形统计图(2)补充完整;
(3)试估计该校2400名学生中参加篮球和羽毛球的学生人数共有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com