
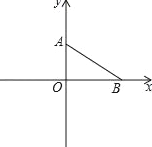
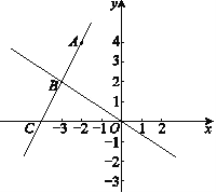
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊA(0ЃЌm)ЁЂB(nЃЌ0)ЃЌЧв|mЉnЉ3|+![]() ЃН0ЃЌЕуPДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃН0ЃЌЕуPДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
(1)ЧѓOAЁЂOBЕФГЄЃЛ
(2)СЌНгPBЃЌЩшЁїPOBЕФУцЛ§ЮЊSЃЌгУtЕФЪНзгБэЪОSЃЛ
(3)Й§ЕуPзїжБЯпABЕФДЙЯпЃЌДЙзуЮЊDЃЌжБЯпPDгыxжсНЛгкЕуEЃЌдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌЪЧЗёДцдкетбљЕФЕуPЃЌЪЙЁїEOPЁеЁїAOBЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)OA=6ЃЌOB=3ЃЛ(2)SЃН![]() |6Љt|(tЁн0)ЃЛ(3)tЃН3Лђ9ЃЎ
|6Љt|(tЁн0)ЃЛ(3)tЃН3Лђ9ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЫуЪѕЦНЗНИљКЭОјЖджЕЕФЗЧИКаджЪМДПЩЧѓЕУmЁЂnЕФжЕЃЌМДПЩНтЬтЃЛ
ЃЈ2ЃЉСЌНгPBЃЌtУыКѓЃЌПЩЧѓЕУOPЃН6ЉtЃЌМДПЩЧѓЕУSЕФжЕЃЛ
ЃЈ3ЃЉзїГіЭМаЮЃЌвзжЄЁЯOBAЃНЁЯOPEЃЌжЛвЊOPЃНOBЃЌМДПЩЧѓжЄЁїEOPЁеЁїAOBЃЌЗжСНжжЧщаЮЧѓЕУtЕФжЕЃЌМДПЩНтЬтЃЎ
(1)Ёп|mЉnЉ3|+![]() ЃН0ЃЌ
ЃН0ЃЌ
Чв|mЉnЉ3|Ён0ЃЌ![]() Ён0
Ён0
Ёр|mЉnЉ3|ЃН![]() ЃН0ЃЌ
ЃН0ЃЌ
ЁрnЃН3ЃЌmЃН6ЃЌ
ЁрЕуA(0ЃЌ6)ЃЌЕуB(3ЃЌ0)ЃЛ
(2)СЌНгPBЃЌ

tУыКѓЃЌAPЃНtЃЌOPЃН|6Љt|ЃЌ
ЁрSЃН![]() OPOBЃН
OPOBЃН![]() |6Љt|ЃЛ(tЁн0)
|6Љt|ЃЛ(tЁн0)
(3)зїГіЭМаЮЃЌ
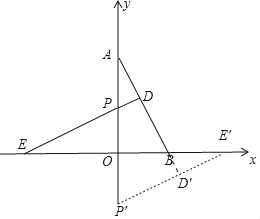
ЁпЁЯOAB+ЁЯOBAЃН90ЁуЃЌЁЯOAB+ЁЯAPDЃН90ЁуЃЌЁЯOPEЃНЁЯAPDЃЌ
ЁрЁЯOBAЃНЁЯOPEЃЌ
ЁржЛвЊOPЃНOBЃЌМДПЩЧѓжЄЁїEOPЁеЁїAOBЃЌ
ЁрAPЃНAOЉOPЃН3ЃЌЛђAPЁфЃНOA+OPЁфЃН9
ЁрtЃН3Лђ9ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
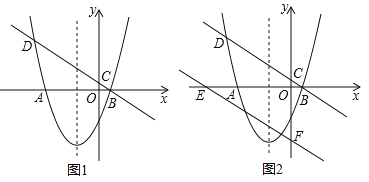
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпy=ax2+2x+cгыxжсНЛгкAЃЈЉ4ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉСНЕуЃЌЙ§ЕуBЕФжБЯпy=kx+![]() ЗжБ№гыyжсМАХзЮяЯпНЛгкЕуCЃЌDЃЎ
ЗжБ№гыyжсМАХзЮяЯпНЛгкЕуCЃЌDЃЎ
ЃЈ1ЃЉЧѓжБЯпКЭХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЖЏЕуPДгЕуOГіЗЂЃЌдкxжсЕФИКАыжсЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЌЕБtЮЊКЮжЕЪБЃЌЁїPDCЮЊжБНЧШ§НЧаЮЃПЧыжБНгаДГіЫљгаТњзуЬѕМўЕФtЕФжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌНЋжБЯпBDбиyжсЯђЯТЦНвЦ4ИіЕЅЮЛКѓЃЌгыxжсЃЌyжсЗжБ№НЛгкEЃЌFСНЕуЃЌдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуMЃЌдкжБЯпEFЩЯЪЧЗёДцдкЕуNЃЌЪЙDM+MNЕФжЕзюаЁЃПШєДцдкЃЌЧѓГіЦфзюаЁжЕМАЕуMЃЌNЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭЈбЖЙЋЫОЭЦГіЂйЃЌЂкСНжжЭЈбЖЪеЗбЗНЪНЙЉгУЛЇбЁдёЃЌЦфжавЛжжгадТзтЗбЃЌСэвЛжжЮодТзтЗбЃЌЧвСНжжЪеЗбЗНЪНЕФЭЈбЖЪБМфx(Зж)гыЗбгУy(дЊ)жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎ
(1)гадТзтЕФЪеЗбЗНЪНЪЧ________(ЬюЁАЂйЁБЛђЁАЂкЁБ)ЃЌдТзтЗбЪЧ________дЊЃЛ
(2)ЗжБ№ЧѓГіЂйЃЌЂкСНжжЪеЗбЗНЪНжаyгыздБфСПxжЎМфЕФКЏЪ§БэДяЪНЃЛ
(3)ЧыФуИљОнгУЛЇЭЈбЖЪБМфЕФЖрЩйЃЌИјГіОМУЪЕЛнЕФбЁдёНЈвщЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќ![]() жа
жа![]() ЃЌ
ЃЌ![]() ДЙжБЦНЗж
ДЙжБЦНЗж![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛЖЏЕуЃЌШє
ЩЯЕФвЛЖЏЕуЃЌШє![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФжмГЄзюаЁжЕЪЧЃЈ ЃЉ
ЕФжмГЄзюаЁжЕЪЧЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓОЙ§ЕуAЃЈ
ЕФЭМЯѓОЙ§ЕуAЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЧвгые§БШР§КЏЪ§
ЃЉЃЌЧвгые§БШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуBЃЈ
ЕФЭМЯѓНЛгкЕуBЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ.
ЃЉ.
ЃЈ1ЃЉЧѓ![]() ЕФжЕМАвЛДЮКЏЪ§
ЕФжЕМАвЛДЮКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєвЛДЮКЏЪ§![]() ЕФЭМЯѓгыxжсНЛгкЕуCЃЌЧве§БШР§КЏЪ§
ЕФЭМЯѓгыxжсНЛгкЕуCЃЌЧве§БШР§КЏЪ§![]() ЕФЭМЯѓЯђЯТЦНвЦmЃЈm>0ЃЉИіЕЅ
ЕФЭМЯѓЯђЯТЦНвЦmЃЈm>0ЃЉИіЕЅ
ЮЛГЄЖШКѓОЙ§ЕуCЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉжБНгаДГіЙигкxЕФВЛЕШЪН![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§y=kx+bЕФЭМЯѓОЙ§ЕуAЃЈЁЊ1ЃЌЁЊ5ЃЉЃЌЧвгые§БШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгкЕуBЃЈ2ЃЌaЃЉЃЎ
ЕФЭМЯѓЯрНЛгкЕуBЃЈ2ЃЌaЃЉЃЎ
ЃЈ1ЃЉЧѓaЕФжЕЃЛ
ЃЈ2ЃЉЧѓвЛДЮКЏЪ§y=kx+bЕФБэДяЪНЃЛ
ЃЈ3ЃЉдкЭЌвЛзјБъЯЕжаЃЌЛГіетСНИіКЏЪ§ЕФЭМЯѓЃЌВЂЧѓетСНЬѕжБЯпгыyжсЮЇГЩЕФШ§НЧаЮЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіе§ећЪ§ФмБэЪОГЩСНИіСЌајХМЪ§ЕФЦНЗНВюЃЌФЧУДГЦетИіе§ећЪ§ЮЊЁАЧЩЪ§ЁБЃЌШчЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвђДЫ4,12,20етШ§ИіЪ§ЖМЪЧЁАЧЩЪ§ЁБ.
ЃЌвђДЫ4,12,20етШ§ИіЪ§ЖМЪЧЁАЧЩЪ§ЁБ.
ЃЈ1ЃЉ400КЭ2020етСНИіЪ§ЪЧЁАЧЩЪ§ЁБТ№ЃПЮЊЪВУДЃП
ЃЈ2ЃЉЩшСНИіСЌајХМЪ§ЮЊ![]() КЭ
КЭ![]() ЃЈЦфжа
ЃЈЦфжа![]() ШЁе§ећЪ§ЃЉЃЌгЩетСНИіСЌајХМЪ§ЙЙдьЕФЁАЧЩЪ§ЁБЪЧ4ЕФБЖЪ§Т№ЃПЮЊЪВУДЃП
ШЁе§ећЪ§ЃЉЃЌгЩетСНИіСЌајХМЪ§ЙЙдьЕФЁАЧЩЪ§ЁБЪЧ4ЕФБЖЪ§Т№ЃПЮЊЪВУДЃП
ЃЈ3ЃЉЧѓНщгк50ЕН101жЎМфЫљгаЁАЧЩЪ§ЁБжЎКЭ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
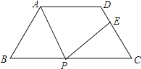
ЁОЬтФПЁПШчЭМЃЌдкЕШбќЬнаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЯТЕз
ЮЊЯТЕз![]() ЩЯвЛЕуЃЈВЛгыЕу
ЩЯвЛЕуЃЈВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїЩфЯп
зїЩфЯп![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ________ЃЎ
________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЬЃЌввЙЄГЬЖгЕЅЖРЯШзі10ЬьКѓЃЌдйгЩМзЁЂввСНИіЙЄГЬЖгКЯзї20ЬьОЭФмЭъГЩШЋВПЙЄзїЃЌвбжЊМзЙЄГЬЖгЕЅЖРЭъГЩДЫЙЄГЬЫљашЬьЪ§ЪЧввЙЄГЬЖгЕЅЖРЭъГЩДЫЙЄГЬЫљашЬьЪ§ЕФ![]() .
.
ЃЈ1ЃЉЧѓМзЁЂввЙЄГЬЖгЕЅЖРЭъГЩДЫЙЄГЬИїашЖрЩйЬьЃЛ
ЃЈ2ЃЉМзЙЄГЬЖгУПЬьЕФЗбгУЮЊ0.67ЭђдЊЃЌввЙЄГЬУПЬьЕФЗбгУЮЊ0.33ЭђдЊЃЌИУЙЄГЬЕФдЄЫуЗбгУЮЊ20ЭђдЊЃЌШєМзЁЂввЙЄГЬЖгвЛЦ№КЯзїЭъГЩИУЙЄГЬЃЌЧыЮЪЙЄГЬЗбгУЪЧЗёЙЛгУЃПШєВЛЙЛгУЃЌгІзЗМгЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com