
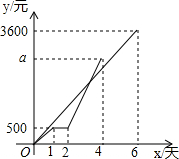
 甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题:
甲、乙两专卖店某段时间内销售收入y(元)与天数x(天)的函数图象如图,在这期间乙专卖店因故停业一天,重新开业后,乙专卖店的日均销售收入是原来的2倍,请解决下列问题:分析 (1)设甲专卖店销售收入y(元)与天数x(天)之间的函数关系式为:y=kx(k≠0),把点(6,3600)代入y=kx+b,即可解答;
(2)装修前乙专卖店的日均销售收入是500÷1=500(元),因为乙专卖店重新开业后的日均销售收入是原来的2倍,所以$\frac{a-500}{4-2}=\frac{500}{1}×2$,解得:a=2500.
(3)甲专卖店销售收入y(元)与天数x(天)之间的函数关系式为:y=600x,装修前,乙店的销售收入y与天数x的函数关系式为y=500x,(0≤x≤1);装修中,乙店的销售收入y与天数x的函数关系式为y=500(1<x≤2);乙店重新开业后,乙店的销售收入y与天数x的函数关系式为:y=500+1000(x-2)=1000x-1500,(2<x≤4);分三种情况进行讨论,即可解答.
解答 解:(1)设甲专卖店销售收入y(元)与天数x(天)之间的函数关系式为:y=kx(k≠0),
把点(6,3600)代入y=kx+b得:3600=6k,
解得:k=600,
∴y=600x,
故答案为:y=600x.
(2)由图可知,当x=1时,y=500,
∴装修前乙专卖店的日均销售收入是500÷1=500(元),
∵乙专卖店重新开业后的日均销售收入是原来的2倍,
以$\frac{a-500}{4-2}=\frac{500}{1}×2$,解得:a=2500.
(3)甲专卖店销售收入y(元)与天数x(天)之间的函数关系式为:y=600x,
装修前,乙店的销售收入y与天数x的函数关系式为y=500x,(0≤x≤1)
装修中,乙店的销售收入y与天数x的函数关系式为y=500(1<x≤2)
乙店重新开业后,乙店的销售收入y与天数x的函数关系式为:
y=500+1000(x-2)=1000x-1500,(2<x≤4)
当0≤x≤1时,600x+500x=30500.解得$\frac{305}{11}$.舍去.
当1<x≤2时,600x+500=30500.解得x=50.舍去.
当2<x≤4时,600x+1000x-1500=30500.解得x=20.
答:经过20天,甲、乙两店销售收入合在一起刚好达到3.05万元
点评 本题考查了一次函数的实际应用,解决本题的关键是得到甲专卖店销售收入y(元)与天数x(天)之间的函数关系式,乙店的销售收入y与天数x的函数关系式,进行分类讨论.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
| A. | x=-9 | B. | x=9 | C. | x=3 | D. | $x=\frac{9}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
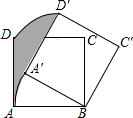 如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.
如图,正方形ABCD边长为3,将正方形ABCD绕点B顺时针旋转30°,得到正方形A′BC′D′,则图中阴影部分的面积是 $\frac{3}{4}π$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
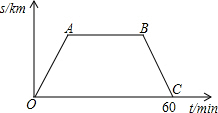 星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA-AB-BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com