
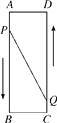
����Ŀ����ͼ����֪A��B��C��DΪ���ε��ĸ����㣬AB��16 cm��AD��6 cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��3 cm/s���ٶ����B�ƶ���һֱ����BΪֹ����Q��2 cm/s���ٶ����D�ƶ�������Pֹͣ�˶�ʱ����QҲֹͣ�˶����ʣ�
(1)P��Q����ӿ�ʼ�����ʱ��ʱ���ı���PBCQ�������33 cm2?
(2)P��Q����ӿ�ʼ�����ʱ��ʱ����P���Q֮��ľ�����10 cm?
���𰸡�(1) P��Q����ӿ�ʼ����5sʱ���ı���PBCQ�������33cm2��(2) P��Q����ӿ�ʼ����1.6s��4.8sʱ����P���Q֮��ľ�����10cm.
�����������������(1)��������xsʱ���Ϊ33��Ȼ��������ε�������㷨���г����̣��Ӷ�����𰸣�(2)������Q��QH��AB��H��Ȼ�����PH�ij��ȣ�������Rt��PHQ�Ĺ��ɶ������δ֪����ֵ�ó��𰸣�
����������⣺(1)��P��Q����ӿ�ʼ����xsʱ���ı���PBCQ�������33cm2.
���������![]() ��(16��3x��2x)��6��33��
��(16��3x��2x)��6��33��
���x��5.(3��)��16��3��![]() >5��
>5��
��x��5�������⣮
��P��Q����ӿ�ʼ����5sʱ���ı���PBCQ�������33cm2��
(2)��P��Q����ӿ�ʼ����ysʱ����P��Q֮��ľ�����10cm��
����Q��QH��AB��H��

���QHA��90��.���ı���ABCD�Ǿ��Σ����A����D��90����
���ı���ADQH�Ǿ��Σ���AH��DQ��(16��2y)cm��QH��AD��6cm��
�൱P����H���Ϸ�ʱ��PH��AH��AP��16��2y��3y��(16��5y)(cm)����P����H���·�ʱ��PH��AP��AH��3y��(16��2y)��(5y��16)(cm)�� ��PH��|16��5y|cm.
��Rt��PQH�У����ݹ��ɶ�����PH2��QH2��PQ2��
��(16��5y)2��62��102�����y1��1.6��y2��4.8. ��16��3��![]() ��
��
��y1��1.6��y2��4.8���������⣮
��P��Q����ӿ�ʼ����1.6s��4.8sʱ����P���Q֮��ľ�����10cm��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������л�����Ĵ�ͳ���գ������ڼ��Ҷ��г����ӵ�ϰ�ߣ�ij����ȥ�����۵����ա����ա���ɳ�յ�������Ϊ3��5��2�������г����飬���о���������ȥ���������Ļ����Ͻ�������������20%����ɳ�ռ���10%�������ղ��䣮Ϊ�ٽ����ۣ���ȫ�����Ӱ�װ��������У����A��2�������ա�4�����ա�2����ɳ�գ����B��3�������ա�3�����ա�2����ɳ�գ����C��2�������ա�5�����ա�1����ɳ�գ��������A��C������������200�У����B��C����������210�У�ÿ�������ա����ա���ɳ�յ��ۼ۷ֱ�Ϊ6Ԫ��5Ԫ��4Ԫ����A��B��C������еİ�װ�ѷֱ�Ϊ10Ԫ��12Ԫ��9Ԫ������ۼ�Ϊ���Ӽ۸���ϰ�װ�ѣ�������Щ���ȫ���۳��������۶�Ϊ_____Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˷ḻѧ���Ŀ����������������Ʒ�̵�һ���Թ������ɸ����������������2�������1��������190Ԫ.����3�������2��������330Ԫ.
��1������һ������һ������������Ԫ��
��2�����ݸ�У��ʵ����������������Ʒ�̵�һ���Թ������������100����Ҫ���������������ܷ��ò�����6500Ԫ��������ѧ�����Թ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A�������Ϊ��0��3����B�������Ϊ��-3.0����DΪx���ϵ�һ�����㣬AE��AD����AE=AD������BE��y���ڵ�M
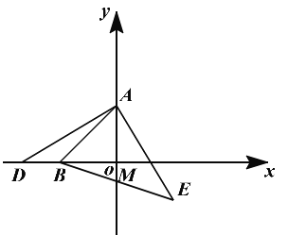
��1����D���������-5.0������E�������:
��2����֤:MΪBE���е�
��3����D����x�����˶�ʱ��̽��:![]() Ϊ��ֵ
Ϊ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
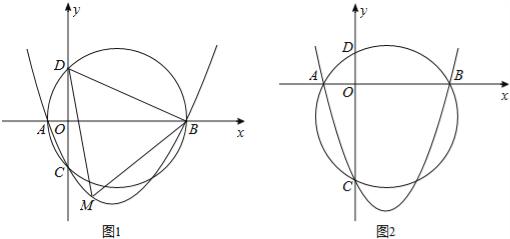
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0��c��0����x���ڵ�A��B����y���ڵ�C�������A��B��C�����Բ��y�����һ������ΪD��
��1����ͼ1����֪��A��B��C������ֱ�Ϊ����2��0������8��0������0����4����
����������ߵı���ʽ���D�����ꣻ
������MΪ�������ϵ�һ���㣬��λ�ڵ������ޣ�����BDM��������ֵ��
��2����ͼ2����a=1����֤������b��cȡ��ֵ����D��Ϊ���㣬����ö������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ��������з��̣�
(1)(6x��1)2��25��
(2)x2��2x��2x��1��
(3)x2��![]() x��2��
x��2��
(4)x(x��7)��8(7��x)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ�������˸���������������������ȫ�淢չ���������Ӱ��ˣ�����ѧУ������ѧ����ѧ��ʱ�涨��ÿѧ�ڶ�ѧ���ĵ������������������������ۺ��������ۣ��ֱ��ǣ������ۺ��������ۡ������ۺ��������ۡ���ĩ�ۺ��������ۣ����꼶��1�����С���Ͱ��꼶��2�����С����λͬѧͬʱ����һ�Ƚ�ѧ����������ǵ������ۺ��������۳ɼ����±���
�����ۺ��������۳ɼ� | �����ۺ��������۳ɼ� | ��ĩ�ۺ��������۳ɼ� | |
�� | 96 | 91 | 92 |
�� | 95 | 93 | 91 |
��1������������ۺ��������۳ɼ��ȶ��ԵĽǶ�������˭���Ե�һ�Ƚ�ѧ������ͨ������ش�
��2����������ۺ��������۳ɼ��������ۺ��������۳ɼ�����ĩ�ۺ��������۳ɼ���![]() �ı����������ճɼ���˭���Ե�һ�Ƚ�ѧ������ͨ������ش�
�ı����������ճɼ���˭���Ե�һ�Ƚ�ѧ������ͨ������ش�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
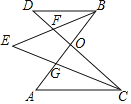
����Ŀ����ͼ��ʾ��AB��CD�ཻ�ڵ�O����BEƽ�֡�ABD��CD��F��CEƽ�֡�ACD��AB��G����A=45������BEC=40�������D�Ķ���Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽ������������״�������人�ȵ�����Ű��Ϊ�˻���������������飬ȫ�����ص�ҽ�ƶ�Ա���ױ���֧Ԯ������ij����ҽԺ��Ҫ8��ҽ����Ա֧Ԯ��Ҫ��ÿ������������ͬ������ÿ��������Ԥ�����������1�ˣ��������ᳬ��100�ˣ���ÿ��������Ԥ�������ٷ���һ�ˣ�����������90�ˣ���ôԤ��ÿ�����������Ƕ����ˣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com