
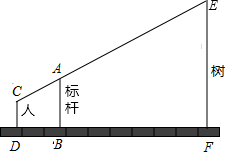
 如图,竖立在点B处的标杆AB 长2.1米,某测量工作人员站在D点处,此时人眼睛C与标杆顶端A、树顶端E在同一直线上(点D、B、F也在同一直线上),已知此人眼睛与地面的距离CD 长1.6米,且BD=1米,BF=5米,求所测量树的高度.
如图,竖立在点B处的标杆AB 长2.1米,某测量工作人员站在D点处,此时人眼睛C与标杆顶端A、树顶端E在同一直线上(点D、B、F也在同一直线上),已知此人眼睛与地面的距离CD 长1.6米,且BD=1米,BF=5米,求所测量树的高度. 分析 作CH⊥EF于点H,交AB于点G,把实际问题抽象到相似三角形中,利用相似三角形的对应边成比例列出方程,解方程即可.
解答  解:作CH⊥EF于点H,交AB于点G;如图所示:
解:作CH⊥EF于点H,交AB于点G;如图所示:
∵AB⊥DF,EF⊥DF,
∴AG∥EH,
∵CH⊥EF,DF⊥EF,CD⊥BD,EF⊥DF,
∴CH=DF,CG=DB,
∵AB=2.1米,CD=1.6米,BD=1米,BF=5米,
∴AG=2.1-1.6=0.5(米),DF=6米,
∵AG∥EH,
∴△ACG∽△ECH,
∴$\frac{AG}{EH}$=$\frac{CG}{CH}$,即$\frac{0.5}{EG}$=$\frac{1}{6}$,
解得:EG=3米,
∴EF=3+1.6=4.6(m)
答:所测量树的高度是4.6米.
点评 本题考查了相似三角形的应用;通过构造相似三角形.利用相似三角形对应边成比例是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
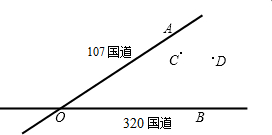 如图:107国道OA和320国道OB在某市交于点O,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站到107国道和320国道距离相等,且PC=PD,请用尺规作图在∠AOB的内部画出货站P的位置.(不写画法,保留画图痕迹,写出结论)
如图:107国道OA和320国道OB在某市交于点O,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站到107国道和320国道距离相等,且PC=PD,请用尺规作图在∠AOB的内部画出货站P的位置.(不写画法,保留画图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
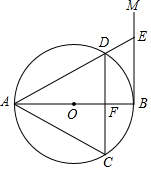 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.
如图,D是直径AB延长线上一点,C是圆O上一点且CO⊥AB,连接CB,DE与圆O相切于E,EF与AB相交于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com