
【题目】如图,在平行四边形![]() 中,
中,![]() 分别为边
分别为边![]() 的中点,
的中点,![]() 是对角线,过点
是对角线,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,
①求证:四边形![]() 是菱形.
是菱形.
②当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.

【答案】(1)见解析;(2)①见解析;②6.
【解析】
(1)由四边形ABCD是平行四边形,可得AB∥CD,AB=CD,又由E、F分别为边AB、CD的中点,易得DF∥BE,DF=BE,即可判定四边形DEBF为平行四边形,则可证得DE∥BF;
(2)①由∠G=90°,AG∥DB,易证得△DBC为直角三角形,又由F为边CD的中点,即可得BF=![]() DC=DF,则可证得:四边形DEBF是菱形;
DC=DF,则可证得:四边形DEBF是菱形;
②根据矩形的判定定理得到四边形AGBD是矩形,根据三角形的面积公式即可得到结论.
证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E、F分别为AB、CD的中点,
∴DF=![]() DC,BE=
DC,BE=![]() AB,
AB,
∴DF∥BE,DF=BE,
∴四边形DEBF为平行四边形,
∴DE∥BF;
(2)①∵AG∥BD,

∴∠G=∠DBC=90°,
∴△DBC为直角三角形,
又∵F为边CD的中点.
∴BF=![]() DC=DF,
DC=DF,
又∵四边形DEBF为平行四边形,
∴四边形DEBF是菱形;
②∵AD∥BG,AG∥BD,∠G=90°,
∴四边形AGBD是矩形,
∴S△ABD=S△ABG=![]() ×3×4=6,
×3×4=6,
∵E为边AB的中点,
∴S△BDE=![]() S△ABD=3,
S△ABD=3,
∴四边形DEBF的面积=2S△BDE=6.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,将放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.
(1)计算AB边的长等于;
(2)在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使矩形的面积等于△ABC的面积,并简要说明画图的方法(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1:对于一个关于![]() 的二次三项式
的二次三项式![]() ,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令
,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令![]() ,然后移项可得:
,然后移项可得:![]() ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定![]() 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:
例:求![]() 的取值范围;
的取值范围;
解:令![]()
![]()
![]()
![]()
![]() ;
;
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ,则关于
,则关于![]() 的一元二次不等式
的一元二次不等式![]() 的解集为:
的解集为:![]() 或
或![]() ;则关于
;则关于![]() 的一元二次不等式的
的一元二次不等式的![]() 的解集为:
的解集为:![]() .
.
材料3:若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ;则
;则![]() ;
;![]() ,我们称之为韦达定理;
,我们称之为韦达定理;
请根据上述材料,解答下列问题:
(1)若关于![]() 的二次三项式
的二次三项式![]() (
(![]() 为常数)的最小值为
为常数)的最小值为![]() ,则
,则![]() ________.
________.
(2)求出代数式![]() 的取值范围.
的取值范围.
(3)若关于![]() 的代数式
的代数式![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )的最小值为
)的最小值为![]() ,最大值为4,请求出满足条件的
,最大值为4,请求出满足条件的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣ ![]()
其中正确的结论个数有( )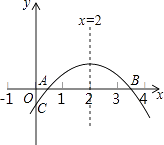
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具店买文具,他与售货员的对话如下:
小明:你好.我要购买5支黑色水笔和3本笔记本.
售货员:好的.那你应该付34元.
小明:我把两种文具的单价弄反了,以为要付46元.
(1)求小明所购买的黑色水笔和笔记本的单价;
(2)如果小红也去购买同样的黑色水笔和笔记本,预算费用不超过88元,并且购买笔记本的数量要比购买黑色水笔的数量多1,那么小红最多能购买多少本笔记本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() cm ,
cm ,![]() cm,过点
cm,过点![]() 作射线
作射线![]() .点
.点![]() 从点
从点![]() 出发,以3 cm/s的速度沿
出发,以3 cm/s的速度沿![]() 匀速移动;点
匀速移动;点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿
cm/s的速度沿![]() 匀速移动.点
匀速移动.点![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止移动.连接
同时停止移动.连接![]() 、
、![]() ,设移动时间为
,设移动时间为![]() (s).
(s).
(1)点![]() 、
、![]() 从移动开始到停止,所用时间为 s;
从移动开始到停止,所用时间为 s;
(2)当![]() 与
与![]() 全等时,
全等时,
①若点![]() 、
、![]() 的移动速度相同,求
的移动速度相同,求![]() 的值;
的值;
②若点![]() 、
、![]() 的移动速度不同,求
的移动速度不同,求![]() 的值;
的值;
(3)如图②,当点![]() 、
、![]() 开始移动时,点
开始移动时,点![]() 同时从点
同时从点![]() 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿![]() 向点
向点![]() 匀速移动,到达点
匀速移动,到达点![]() 后立刻以原速度沿
后立刻以原速度沿![]() 返回.当点
返回.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 、
、![]() 同时停止移动.在移动的过程中,是否存在
同时停止移动.在移动的过程中,是否存在![]() 与
与![]() 全等的情形?若存在,求出
全等的情形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
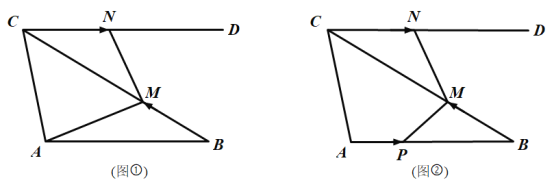
查看答案和解析>>
科目:初中数学 来源: 题型:
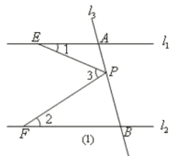
【题目】如图 ,已知直线l1,l2,点P在直线l3上且不与点A、B重合.记∠AEP=∠1,∠BFP=∠2,∠EPF=∠3.
(1) 如图 ,若直线l1//l2,点P在线段AB(A、B两点除外)上运动时,写出∠1、∠2、∠3之间的关系,并说明理由.
(2)如图 ,若(1)中∠1、∠2、∠3之间的关系成立,你能不能反向推出直线l1//l2?若成立请说明理由.
(3)如图 ,若直线l1//l2,若点P在A、B两点外侧运动时(不包括线段AB),请直接写出∠1、∠2、∠3之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com