
分析 如图,由题意图象C2的解析式为y=-(x-2)2,图象C3是图中两根红线之间的C1、C2上的部分图象,分五种情形讨论即可.
解答 解:如图,由题意图象C2的解析式为y=-(x-2)2,图象C3是图中两根红线之间的C1、C2上的部分图象.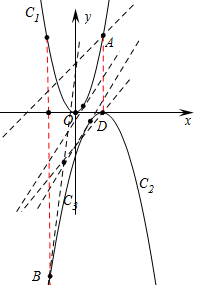
由-2$≤\\;x≤2$x≤2,则A(2,4),B(-2,-16),D(2,0).
因为一次函数y=kx+k-1(k>0)的图象与图象C3有两个交点
①当直线经过点A时,满足条件,4=2k+k-1,解得k=$\frac{5}{3}$,
②当直线与抛物线C1切时,由$\left\{\begin{array}{l}{y={x}^{2}}\\{y=kx+k-1}\end{array}\right.$消去y得到x2-kx-k+1=0,∵△=0,
∴k2+4k-4=0,解得k=$-2+2\sqrt{2}$或-2-2$\sqrt{2}$(舍弃),
观察图象可知当-2+2$\sqrt{2}$<k≤$\frac{5}{3}$时,直线与图象C3有两个交点.
③当直线与抛物线C2相切时,由$\left\{\begin{array}{l}{y=-(x-2)^{2}}\\{y=kx+k-1}\end{array}\right.$,消去y,得到x2-(4-k)x+3+k=0,∵△=0,
∴(4-k)2-4(3+k)=0,解得k=6-4$\sqrt{2}$或6+4$\sqrt{2}$(舍弃),
④当直线经过点D(2,0)时,0=2k+k-1,解得k=$\frac{1}{3}$,
观察图象可知,$\frac{1}{3}$≤k-4$\sqrt{2}$+6时,直线与图象C3有两个交点.
⑤当直线经过点B(-2,-16)时,-16=-2k+k-1,解得k=15,
观察图象可知,k≥15时,直线与图象C3有两个交点.
综上所述,当-2+2$\sqrt{2}$<k≤$\frac{5}{3}$或$\frac{1}{3}$≤k-4$\sqrt{2}$+6或k≥15时,直线与图象C3有两个交点.
故答案为-2+2$\sqrt{2}$<k≤$\frac{5}{3}$或$\frac{1}{3}$≤k-4$\sqrt{2}$+6或k≥15
点评 本题考查二次函数的应用、一次函数的应用、旋转变换、二元二次方程组、根的判别式等知识,解题的关键是求出函数C2的解析式,搞清楚图象C3,学会用转化的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
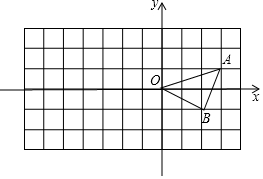 方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:
方格纸中每个小正方形的边长都是单位1,△OAB在平面直角坐标系中的位置如图所示.解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 天安门城楼高度 | B. | 未来北京最高建筑“中国尊”高度 | ||
| C. | 五岳之首泰山高度 | D. | 国际航班飞行高度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
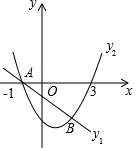 如图,A(-1,0)、B(2,-3)两点在一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象上.
如图,A(-1,0)、B(2,-3)两点在一次函数y1=-x+m与二次函数y2=ax2+bx-3的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com