
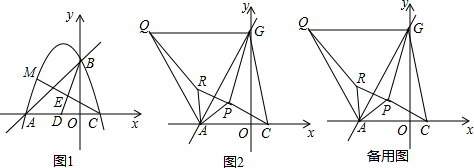
分析 (1)把A(-3,0),B(0,3)代入抛物线y=-x2+bx+c即可解决问题.
(2)首先求出A、C、D坐标,根据BE=2ED,求出点E坐标,求出直线CE,利用方程组求交点坐标M.
(3)①欲证明PG=QR,只要证明△QAR≌△GAP即可.②当Q、R、P、C共线时,PA+PG+PC最小,作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K,由sin∠ACM=$\frac{AM}{AC}$=$\frac{NQ}{QC}$求出AM,CM,利用等边三角形性质求出AP、PM、PC,由此即可解决问题.
解答 解:(1)∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,
∴A(-3,0),B(0,3),
∵抛物线y=-x2+bx+c过A、B两点,
∴$\left\{\begin{array}{l}{c=3}\\{-9-3b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴b=-2,c=3.
(2),对于抛物线y=-x2-2x+3,令y=0,则-x2-2x+3=0,解得x=-3或1,
∴点C坐标(1,0),
∵AD=DC=2,
∴点D坐标(-1,0),
∵BE=2ED,
∴点E坐标(-$\frac{2}{3}$,1),
设直线CE为y=kx+b,把E、C代入得到$\left\{\begin{array}{l}{-\frac{2}{3}k+b=1}\\{k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=\frac{3}{5}}\end{array}\right.$,
∴直线CE为y=-$\frac{3}{5}$x+$\frac{3}{5}$,
由$\left\{\begin{array}{l}{y=-\frac{3}{5}x+\frac{3}{5}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{12}{5}}\\{y=\frac{51}{25}}\end{array}\right.$,
∴点M坐标(-$\frac{12}{5}$,$\frac{51}{25}$).
(3)①∵△AGQ,△APR是等边三角形,
∴AP=AR,AQ=AG,∠QAC=∠RAP=60°,
∴∠QAR=∠GAP,
在△QAR和△GAP中,
$\left\{\begin{array}{l}{AQ=AG}\\{∠QAR=∠GAP}\\{AR=AP}\end{array}\right.$,
∴△QAR≌△GAP,
∴QR=PG.
②如图3中,∵PA+PB+PC=QR+PR+PC=QC,
∴当Q、R、P、C共线时,PA+PG+PC最小,
作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K.
∵∠GAO=60°,AO=3,
∴AG=QG=AQ=6,∠AGO=30°,
∵∠QGA=60°,
∴∠QGO=90°,
∴点Q坐标(-6,3$\sqrt{3}$),
在RT△QCN中,QN=3$\sqrt{3}$,CN=7,∠QNC=90°,
∴QC=$\sqrt{Q{N}^{2}+N{C}^{2}}$=2$\sqrt{19}$,
∵sin∠ACM=$\frac{AM}{AC}$=$\frac{NQ}{QC}$,
∴AM=$\frac{6\sqrt{57}}{19}$,
∵△APR是等边三角形,
∴∠APM=60°,∵PM=PR,cos30°=$\frac{AM}{AP}$,
∴AP=$\frac{12\sqrt{19}}{19}$,PM=RM=$\frac{6\sqrt{19}}{19}$
∴MC=$\sqrt{A{C}^{2}-A{M}^{2}}$=$\frac{14\sqrt{19}}{19}$,
∴PC=CM-PM=$\frac{8\sqrt{19}}{19}$,
∵$\frac{PK}{QN}$=$\frac{CP}{CQ}$=$\frac{CK}{CN}$,
∴CK=$\frac{28}{19}$,PK=$\frac{12\sqrt{3}}{19}$,
∴OK=CK-CO=$\frac{9}{19}$,
∴点P坐标(-$\frac{9}{19}$,$\frac{12\sqrt{3}}{19}$).
∴PA+PC+PG的最小值为2$\sqrt{19}$,此时点P的坐标(-$\frac{9}{19}$,$\frac{12\sqrt{3}}{19}$).
点评 本题考查二次函数综合题、等边三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是理解Q、R、P、C共线时,PA+PG+PC最小,学会添加常用辅助线,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
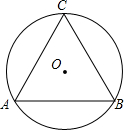 如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )
如图,等边△ABC是⊙O的内接三角形,则圆心O关于直线AB的对称点O′和⊙O的位置关系是( )| A. | 在⊙O内 | B. | 在⊙O上 | C. | 在⊙O外 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
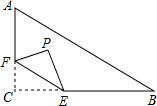 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是1.2.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是1.2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com