
 中,
中, ,
, 为平面内一动点,
为平面内一动点, ,
, ,其中a,b为常数,且
,其中a,b为常数,且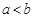 .将
.将 沿射线
沿射线 方向平移,得到
方向平移,得到 ,点A、B、D的对应点分别为点F、C、E.连接
,点A、B、D的对应点分别为点F、C、E.连接 .
. 在
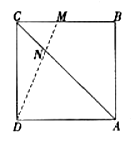
在 内部,请在图1中画出
内部,请在图1中画出 ;
; ,求
,求 的长(用含
的长(用含 的式子表示);
的式子表示); ,当线段
,当线段 的长度最大时,则
的长度最大时,则 的大小为__________;当线段
的大小为__________;当线段 的长度最小时,则
的长度最小时,则 的大小为_______________(用含
的大小为_______________(用含 的式子表示).
的式子表示).
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ”,那么四边形ABCD一定是平行四边形;
”,那么四边形ABCD一定是平行四边形; ”,那么四边形ABCD一定是平行四边形
”,那么四边形ABCD一定是平行四边形| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com