试题分析:(1)先做(2),根据特殊元素法得出结论;(2)构造直角三角形,过A、C点作AD⊥BC交BC的延长线于点D,CE⊥AB于E,根据三角函数知识,可用α表示出AB的长度,再表示出AE和BE的长度,AB=AE+BE,分别让带有α两式相等即可;(3)要求三角形的面积,必须找到三角形的一边和这条边上的高;过点A作AG⊥CD交CD的延长线于G点.根据题意可知CD和AD的长度,和∠ADG的度数,根据上述得出的结论,可以求出∠的正弦值,在直角三角形ADG中,AD已知,根据三角函数关系式即可得出AG的长度,代入S△ADC的面积公式即可.
试题解析:(1)C.
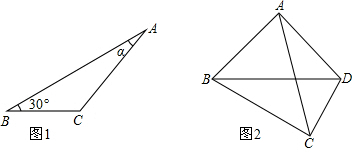
(2)如图1,过点A作AD⊥BC交BC的延长线于点D.
∵∠B=30°,∠BAC=α,AC=1,∴∠ACD=α+30°.
∴在△ADC中,∠ADC=90°,AD=AC•sin∠ACD=sin(α+30°).
∵在△ABD中,∠ADB=90°,∠B=30°,∴AB=2AD=2sin(α+30°).
过点C作CE⊥AB于E.
∴在△CEA中,∠AEC=90°,CE=sinα,AE=cosα.
在△BEC中,∠BEC=90°,

.
∴AB="AE+BE=cosα+"

.
∴

.

(3)由(2)证明的等式易得

.
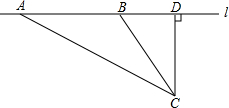
如图2,过点A作AG⊥CD交CD的延长线于点G.
∵△ABD和△BCD是两个含45°和30°的直角三角形,
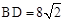
,∴∠ADG=75°,AD=8,CD=

.
∵

.
∴在△ADG中,∠AGD=90°,AG=AD•sin∠ADG=8×sin75°=

.
∴

.


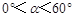 时,下列关系式中有且仅有一个正确.
时,下列关系式中有且仅有一个正确.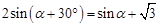
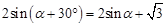
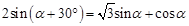
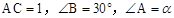 ,请利用此图证明(1)中的结论;
,请利用此图证明(1)中的结论;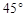 和
和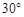 的直角三角板如图2方式放置在同一平面内,
的直角三角板如图2方式放置在同一平面内,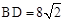 ,求
,求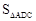 .
.
 .
. .
. .
. .
.
 .
. 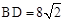 ,∴∠ADG=75°,AD=8,CD=
,∴∠ADG=75°,AD=8,CD= .
. .
. .
. .
.


 );
); )
)