
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.
正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则An的坐标是(2n-1-1,2n-1),.  智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (1,-6) | C. | (-1,6) | D. | (-1,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
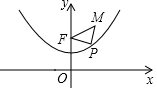 已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )
已知抛物线y=$\frac{1}{4}$x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为($\sqrt{3}$,3),P是抛物线y=$\frac{1}{4}$x2+1上一个动点,则△PMF周长的最小值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinA=$\frac{c}{a}$ | B. | cosB=$\frac{b}{c}$ | C. | sinB=$\frac{b}{a}$ | D. | tanA=$\frac{a}{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,2 | B. | 3,4 | C. | 5,2 | D. | 5,4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com