
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”;
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
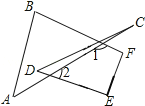
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 .

【答案】360°
【解析】
试题分析:(1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;
(2)根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P=![]() (∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(3)与(2)的证明方法一样得到∠P=![]() (2∠C+∠B).
(2∠C+∠B).
(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.
解:(1)在图2中有3个以线段AC为边的“8字形”,
故答案为3;
(2)∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=∠P﹣∠B,
即∠P=![]() (∠C+∠B),
(∠C+∠B),
∵∠C=100°,∠B=96°
∴∠P=![]() (100°+96°)=98°;
(100°+96°)=98°;
(3)∠P=![]() (β+2α);
(β+2α);
理由:∵∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,
∠CDB,
∴∠BAP=![]() ∠BAC,∠BDP=
∠BAC,∠BDP=![]() ∠BDC,
∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,∠P﹣∠B=
∠BAC,∠P﹣∠B=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,
∠BAC,
∴2(∠C﹣∠P)=∠P﹣∠B,
∴∠P=![]() (∠B+2∠C),
(∠B+2∠C),
∵∠C=α,∠B=β,
∴∠P=![]() (β+2α);
(β+2α);
(4)∵∠B+∠A=∠1,∠C+∠D=∠2,
∴∠A+∠B+∠C+∠D=∠1+∠2,
∵∠1+∠2+∠F+∠E=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360°.


科目:初中数学 来源: 题型:
【题目】已知三角形的两边长是2 cm,3 cm,则该三角形的周长l的取值范围是( )
A. 1<l<5 B. 1<l<6
C. 5<l<9 D. 6<l<10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)= ;
(2)(x﹣1)(x2+x+1)= ;
(3)(x﹣1)(x3+x2+x+1)= ;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件,分别求出对应的二次函数的关系式.
(1)已知二次函数的图象经过点A(0,-1),B(1,0),C(-1,2);
(2)已知抛物线的顶点为(1,-3),且与y轴交于点(0,1);
(3)已知抛物线与x轴交于点M(-3,0),(5,0),且与y轴交于点(0,-3);
(4)已知抛物线的顶点为(3,-2),且与x轴两交点间的距离为4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A. 最高分 B. 平均数 C. 中位数 D. 方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com