
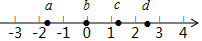 实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | a | B. | b | C. | c | D. | d |
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
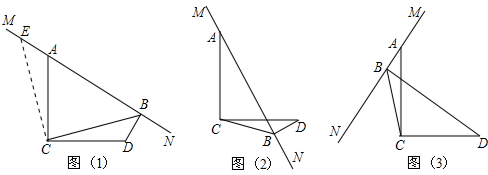
| 过点C作CE⊥CB于点C,与MN交于点E ∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°, ∴∠BCD=∠ACE. ∵四边形ACDB内角和为360°, ∴∠BDC+∠CAB=180°. ∵∠EAC+∠CAB=180°, ∴BD+AB=$\sqrt{2}$CB. | ∴∠EAC=∠BDC 又∵AC=DC, ∴△ACE≌△DCB, ∴AE=DB,CE=CB, ∴△ECB为等腰直角三角形, ∴BE=$\sqrt{2}$CB. 又∵BE=AE+AB, ∴BE=BD+AB. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
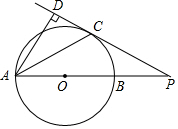 如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB.
如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com