
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;②BF⊥EN;③△BEN是等边三角形;④S△BEF=3S△DEF.其中,将正确结论的序号全部选对的是( )

A. ①②③
B. ①②④
C. ②③④
D. ①②③④
【答案】B
【解析】试题分析:∵四边形ABCD是矩形,∴∠D=∠BCD=90°,由折叠的性质可得:∠EMF=∠D=90°,DF=MF,
即FM⊥BE,CF⊥BC, ∵BF平分∠EBC, ∴CF=MF, ∴DF=CF;故①正确;
∵∠BFM=90°﹣∠EBF,∠BFC=90°﹣∠CBF, ∴∠BFM=∠BFC, ∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN, ∵∠BFE+∠BFN=180°, ∴∠BFE=90°, 即BF⊥EN,故②正确;
∵在△DEF和△CNF中,∠D=∠FCN=90°,DF=CF,∠DFE=∠CFN∴△DEF≌△CNF(ASA),
∴EF=FN, ∴BE=BN, 但无法求得△BEN各角的度数, ∴△BEN不一定是等边三角形;故③错误;
∵∠BFM=∠BFC,BM⊥FM,BC⊥CF, ∴BM=BC=AD=2DE=2EM, ∴BE=3EM,
∴S△BEF=3S△EMF=3S△DEF;∴④正确.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】如图所示,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F, ∠1+∠2=90°.

(1)AB与CD平行吗?试说明理由.
(2)试探究∠2与∠3的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边△ABC中,点H在边BC上,点K在边AC上,且满足AK=HC,连接AH、BK交于点F.
(1)如图1,求∠AFB的度数;
(2)如图2,连接FC,若∠BFC=90°,点G为边 AC上一点,且满足∠GFC=30°,求证:AG⊥BG
(3)如图3,在(2)条件下,在BF上取D使得DF=AF,连接CD交AH于E,若△DEF面积为1, 则△AHC的面积为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A,B两点,点A在点B的左边,与y轴交于点C,顶点为D,若以BD为直径的⊙M经过点C.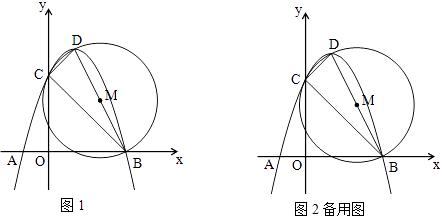
(1)请直接写出C,D两点的坐标(用含a的代数式表示);
(2)求抛物线的函数表达式;
(3)在抛物线上是否存在点E,使∠EDB=∠CBD?若存在,请求出所有满足条件的点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD 中,E、F 两点在对角线 BD 上,BE=DF.
(1) 求证:AE=CF;
(2) 当四边形AECF 为矩形时,直接写出![]()
![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是cm.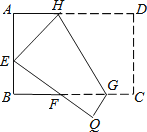
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com