



科目:初中数学 来源: 题型:
 (2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).
(2013•池州一模)我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).查看答案和解析>>
科目:初中数学 来源:三点一测丛书八年级数学上 题型:044
我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图(1))

探索下列问题:
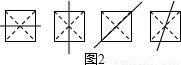
(1)在图(2)给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成![]() 角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
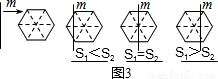
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.
①请你在图中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);

②请你在图中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接).

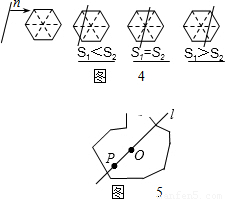
(3)是否存在一条直线将一个任意的平面图形(如图)分割成面积相等的两部分?请简略说出理由.

查看答案和解析>>
科目:初中数学 来源:中考必备’04全国中考试题集锦·数学 题型:059
我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分(如图1).

探索下列问题:
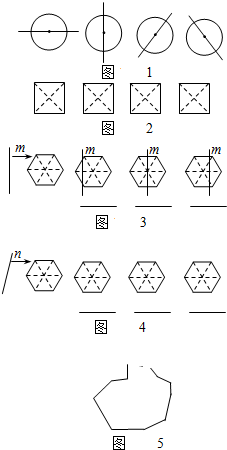
(1)在图2给出的四个正方形中,各画出一条直线(依次是:水平方向的直线、竖直方向的直线、与水平方向成45°角的直线和任意的直线),将每个正方形都分割成面积相等的两部分;
![]()
(2)一条竖直方向的直线m以及任意的直线n,在由左向右平移的过程中,将正六边形分成左右两部分,其面积分别记为S1和S2.

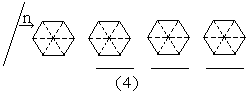
①请你在图3中相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接);
②请你在图4中分别画出反映S1与S2三种大小关系的直线n,并在相应图形下方的横线上分别填写S1与S2的数量关系式(用“<”,“=”,“>”连接=.
(3)是否存在一条直线,将一个任意的平面图形(如图5)分割成面积相等的两部分?请简略说出理由.

查看答案和解析>>
科目:初中数学 来源:同步题 题型:操作题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com