
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
(1)y=﹣x2﹣2x+3
(2)点F的坐标为( ,
, )
)
(3)当t为 秒或2秒或3秒或
秒或2秒或3秒或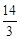 秒时,以P、B、C为顶点的三角形是直角三角形。
秒时,以P、B、C为顶点的三角形是直角三角形。
解析试题分析:(1)先由直线AB的解析式为y=x+3,求出它与x轴的交点A、与y轴的交点B的坐标,再将A、B两点的坐标代入y=﹣x2+bx+c,运用待定系数法即可求出抛物线的解析式。
∵y=x+3与x轴交于点A,与y轴交于点B,
∴当y=0时,x=﹣3,即A点坐标为(﹣3,0),当x=0时,y=3,即B点坐标为(0,3)。
将A(﹣3,0),B(0,3)代入y=﹣x2+bx+c,得 ,解得
,解得 。
。
∴抛物线的解析式为y=﹣x2﹣2x+3。
(2)设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),运用配方法求出抛物线的对称轴及顶点D的坐标,再设抛物线的对称轴与x轴交于点G,连接FG,根据S△AEF=S△AEG+S△AFG﹣S△EFG=3,列出关于m的方程,解方程求出m的值,进而得出点F的坐标。
如图1,设第三象限内的点F的坐标为(m,﹣m2﹣2m+3),
则m<0,﹣m2﹣2m+3<0。
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴对称轴为直线x=﹣1,顶点D的坐标为(﹣1,4)。
设抛物线的对称轴与x轴交于点G,连接FG,
则G(﹣1,0),AG=2。
∵直线AB的解析式为y=x+3,
∴当x=﹣1时,y=﹣1+3=2。∴E点坐标为(﹣1,2)。
∵S△AEF=S△AEG+S△AFG﹣S△EFG
= ×2×2+
×2×2+ ×2×(m2+2m﹣3)﹣
×2×(m2+2m﹣3)﹣ ×2×(﹣1﹣m)=m2+3m,
×2×(﹣1﹣m)=m2+3m,
∴以A、E、F为顶点的三角形面积为3时,m2+3m=3,
解得m1= ,m2=
,m2= (舍去)。
(舍去)。
当m= 时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m=
时,﹣m2﹣2m+3=﹣m2﹣3m+m+3=﹣3+m+3=m= 。
。
∴点F的坐标为( ,
, )。
)。
(3)设P点坐标为(﹣1,n),.
∵B(0,3),C(1,0),∴BC2=12+32=10。
分三种情况:
①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,
即(0+1)2+(n﹣3)2+10=(1+1)2+(n﹣0)2,
化简整理得6n=16,解得n=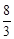 。
。
∴P点坐标为(﹣1,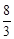 )。
)。
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣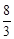 =
= 。
。
∵点P的速度为每秒1个单位长度,∴t1= 秒。
秒。
②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,
即(0+1)2+(n﹣3)2+(1+1)2+(n﹣0)2=10,
化简整理得n2﹣3n+2=0,解得n=2或1。
∴P点坐标为(﹣1,2)或(﹣1,1),
∵顶点D的坐标为(﹣1,4),
∴PD=4﹣2=2或PD=4﹣1=3。
∵点P的速度为每秒1个单位长度,∴t2=2秒,t3=3秒。
③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,
即10+(1+1)2+(n﹣0)2=(0+1)2+(n﹣3)2,
化简整理得6n=﹣4,解得n= 。
。
∴P点坐标为(﹣1, )。
)。
∵顶点D的坐标为(﹣1,4),∴PD=4+ =
=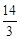 。
。
∵点P的速度为每秒1个单位长度,
∴t4=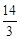 秒。
秒。
综上所述,当t为 秒或2秒或3秒或
秒或2秒或3秒或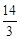 秒时,以P、B、C为顶点的三角形是直角三角形。
秒时,以P、B、C为顶点的三角形是直角三角形。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
中秋节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.
九(1)班数学建模兴趣小组根据调查,整理出第x天( )的捕捞与销售的相关信息如下:
)的捕捞与销售的相关信息如下:
| 鲜鱼销售单价(元/kg) | 20 |
| 单位捕捞成本(元/kg) |  |
| 捕捞量(kg) | 950-10x |
 日捕捞成本)
日捕捞成本)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线抛物线 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
①若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价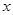 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元
请比较哪种方案的最大利润更高,并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图.在平面直角坐标系中,边长为 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.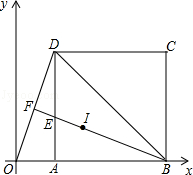
(1)求证:△OAD≌△EAB;
(2)求过点O、E、B的抛物线所表示的二次函数解析式;
(3)在(2)中的抛物线上是否存在点P,其关于直线BF的对称点在x轴上?若有,求出点P的坐标;
(4)连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,二次函数 的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(
的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(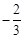 ,0),以OC为直径作半圆,圆心为D.
,0),以OC为直径作半圆,圆心为D.
(1)求二次函数的解析式;
(2)求证:直线BE是⊙D的切线;
(3)若直线BE与抛物线的对称轴交点为P,M是线段CB上的一个动点(点M与点B,C不重合),过点M作MN∥BE交x轴与点N,连结PM,PN,设CM的长为t,△PMN的面积为S,求S与t的函数关系式,并写出自变量t的取值范围.S是否存在着最大值?若存在,求出最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知二次函数 (m>0)的图象与x轴交于A、B两点.
(m>0)的图象与x轴交于A、B两点.
(1)写出A、B两点的坐标(坐标用m表示);
(2)若二次函数图象的顶点P在以AB为直径的圆上,求二次函数的解析式;
(3)设以AB为直径的⊙M与y轴交于C、D两点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线 的图象过C点.
的图象过C点.
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?
(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点(点A在点B的左侧)。
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com