
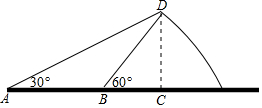
 如图,由山脚下的一点A测得山顶D的仰角是30°,从A前进100米到B,再次测得山顶D的仰角为60°,求山高CD的高度(结果精确到0.1米).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,由山脚下的一点A测得山顶D的仰角是30°,从A前进100米到B,再次测得山顶D的仰角为60°,求山高CD的高度(结果精确到0.1米).(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 分析 设CD=xm,利用正切的定义分别得到AC=$\frac{x}{tan30°}$=$\sqrt{3}$x,BC=$\frac{x}{tan60°}$=$\frac{\sqrt{3}}{3}$x,则$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=100,然后解方程即可.
解答 解:设CD=xm,
在Rt△ACD中,∵tanA=$\frac{CD}{AC}$,
∴AC=$\frac{x}{tan30°}$=$\sqrt{3}$x,
在Rt△BCD中,∵tan∠CBD=$\frac{CD}{BC}$,
∴BC=$\frac{x}{tan60°}$=$\frac{\sqrt{3}}{3}$x,
而AC-BC=AB,
∴$\sqrt{3}$x-$\frac{\sqrt{3}}{3}$x=100,
∴x=50$\sqrt{3}$≈86.6(m).
答:山高CD的高度为86.6米.
点评 本题考查了解直角三角形的应用-仰角俯角问题:正确理解仰角与俯角的定义,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:解答题
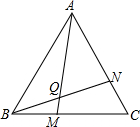 学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求证:∠BQM=60°
学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M、N分别在等边△ABC的BC、CA边上,且BM=CN,AM、BN交于点Q,求证:∠BQM=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
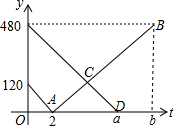 甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的0.75,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.
甲乙两城市之间有一条公路相连,公路中途穿过丙市,现有两位司机M、N相约各自同时从甲乙两地出发,途中M将一件物品交给N,已知M从甲市到丙市,N从乙市到甲市,N的速度是M的0.75,他们开车距离丙市的距离y(千米)与行驶的时间t(小时)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
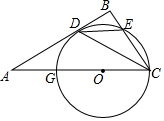 如图,点O为Rt△ABC斜边AC上一点,以点O为圆心,OC长为半径的⊙O与AB相切于点D,分别交AC,BC于点G,E.
如图,点O为Rt△ABC斜边AC上一点,以点O为圆心,OC长为半径的⊙O与AB相切于点D,分别交AC,BC于点G,E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
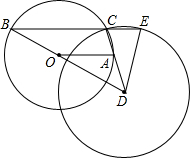 如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.
如图,在⊙O中,半径OA长为1,弦BC∥OA,射线BO,射线CA交于点D,以点D为圆心,CD为半径的⊙D交BC延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com