
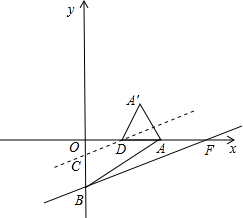
 ��֪A��2$\sqrt{3}$��0����ֱ��y=��2-$\sqrt{3}$��x-2��x�ύ�ڵ�F����y�ύ�ڵ�B��ֱ��l��AB�ҽ�y���ڵ�C����x���ڵ�D����A����ֱ��l�ĶԳƵ�ΪA�䣬����AA�䡢A��D��ֱ��l��AB��������ÿ��1����λ���ٶ���y������������ƽ�ƣ����ƶ�ʱ��Ϊt��
��֪A��2$\sqrt{3}$��0����ֱ��y=��2-$\sqrt{3}$��x-2��x�ύ�ڵ�F����y�ύ�ڵ�B��ֱ��l��AB�ҽ�y���ڵ�C����x���ڵ�D����A����ֱ��l�ĶԳƵ�ΪA�䣬����AA�䡢A��D��ֱ��l��AB��������ÿ��1����λ���ٶ���y������������ƽ�ƣ����ƶ�ʱ��Ϊt������ ��1����ȷ��B�����꣬�����ô���ϵ�������ֱ��AB�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x-2�����õ�ƽ�Ƶ�������ɵõ�C��0��t-2������ֱ��l�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+t-2����ɵõ�D��2$\sqrt{3}$-$\sqrt{3}$t��0�������ǿɼ����AD=$\sqrt{3}$t����֤����A��DAΪ�ȱ������Σ�Ȼ��ȷ��A�������ꣻ
��2�������F�����꣬Ȼ������AB��AF�ij����Ӷ��õ�AB=AF��
��3����ͼ2�����������ߵ��ж������õ�����C��AD��x�ᣩ����ʱ��Ҳһ����A��D���У���֤��CB=CE���Ӷ��õ���C�İ뾶Ϊ2-t��Ȼ�����ۣ�����C��AD���У������������ʵ�2-t=t������C��AA������ʱ��l��AA���ཻ��M����ͼ2�������������ʵ�t=$\frac{3}{2}$t-2��t-2�������ֱ�ⷽ�����t���ɣ�
��� ��1���⣺��x=0ʱ��y=��2-$\sqrt{3}$��x-2=-2����B��0��-2����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��A��2$\sqrt{3}$��0����B��0��-2�������$\left\{\begin{array}{l}{2\sqrt{3}k+b=0}\\{b=-2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=-2}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x-2��
��OB=2��OA=2$\sqrt{3}$��
���OAB=30�㣬
�ߵ�B����ƽ��t����λ��
��C��0��t-2����
��ֱ��l�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+t-2��
��y=0ʱ��-$\frac{\sqrt{3}}{3}$x+t-2=0�����x=2$\sqrt{3}$-$\sqrt{3}$t����D��2$\sqrt{3}$-$\sqrt{3}$t��0����
��AD=$\sqrt{3}$t��
�ߵ�A����ֱ��l�ĶԳƵ�ΪA������l��AB��
��DA��=DA����A��DA=2��OAB=60�㣬
���A��DAΪ�ȱ������Σ�
��A��H��DA����ͼ1��
��A��H=$\frac{\sqrt{3}}{2}$DA=$\frac{3}{2}$t��DH=AH=$\frac{\sqrt{3}}{2}$t��
��A����2$\sqrt{3}$-$\frac{\sqrt{3}t}{2}$��$\frac{3t}{2}$����
��2��֤������y=0ʱ����2-$\sqrt{3}$��x-2=0�����x=4+2$\sqrt{3}$����F��4+2$\sqrt{3}$��0����
��A��2$\sqrt{3}$��0����B��0��-2����
��AF=4��AB=4��
��AB=AF��
��3���⣺��ͼ2��
��ֱ��l�ǵ�A��A���ĶԳ��ᣬ
��ֱ��l�ǡ�A��DA��ƽ���ߣ�
���C��ֱ��AD��A��D�ľ�����ȣ�
�൱��C��AD��x�ᣩ����ʱ��Ҳһ����A��D���У�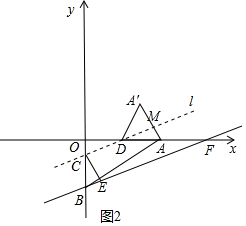
�ߡ�OAB=30����AB=AF��
���ABF=15�㣬
�ߡ�OBA=60�㣬
���CBF=75�㣬
��CE��AB��
���BCE=30�㣬
���CEB=180��-30��-75��=75�㣬
��CB=CE��
���C�İ뾶Ϊ2-t��
����C��AD����CO=CB����2-t=t�����t=1��
����C��AA������ʱ��l��AA���ཻ��M����ͼ2����CB=CM��t=$\frac{3}{2}$t-2��t-2�������t=$\frac{8}{3}$��
��������������Ҫ���t��ֵ��������t=1��$\frac{8}{3}$��
���� ���⿼����Բ���ۺ��⣺����������ֱ��ƽ�е����ʡ��ȱ������ε��ж������ʺ����ߵ��ж������ʣ������ô���ϵ������ֱ�߽���ʽ������ֱ����������Ľ������꣬����������ͼ�����ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=5��AC=7��BOƽ�֡�ABC��COƽ�֡�ACB��MN������O����AB��AC�ཻ�ڵ�M��N����MN��BC�����AMN���ܳ�����12��
��ͼ����ABC�У�AB=5��AC=7��BOƽ�֡�ABC��COƽ�֡�ACB��MN������O����AB��AC�ཻ�ڵ�M��N����MN��BC�����AMN���ܳ�����12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �������ϱ�ʾ���и��������á������Ű����ǰ��մ�С�����˳�����У�
�������ϱ�ʾ���и��������á������Ű����ǰ��մ�С�����˳�����У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ABC����ABΪһ����ABP��ʹ֮���ABCȫ�ȣ��ڷ���ֽ�У��������з��������ġ�ABP��
��ͼ����֪��ABC����ABΪһ����ABP��ʹ֮���ABCȫ�ȣ��ڷ���ֽ�У��������з��������ġ�ABP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
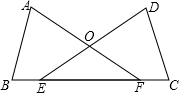 ��ͼ����E��F���߶�BC�ϣ�BE=CF����A=��D����B=��C��AF��DE���ڵ�O����֤����ABF�ա�DCE��
��ͼ����E��F���߶�BC�ϣ�BE=CF����A=��D����B=��C��AF��DE���ڵ�O����֤����ABF�ա�DCE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ɼ�����ͬ��С�����������ɵļ���������濴����״ͼ��С�������е����ֱ�ʾ�ڸ�λ���ϵ�С�������ĸ������뻭���������ͼ�����濴�����濴����״ͼ��
��ͼ���ɼ�����ͬ��С�����������ɵļ���������濴����״ͼ��С�������е����ֱ�ʾ�ڸ�λ���ϵ�С�������ĸ������뻭���������ͼ�����濴�����濴����״ͼ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com