
 如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.分析 (1)依据k=tan∠COA进行求解即可;
(2)如图1所示:过点P作PD⊥OA,垂足为D.由锐角三角函数的定义和特殊锐角三角函数值可求得PD=$\frac{\sqrt{3}t}{2}$,然后利用三角形的面积公式列出关系式,最后利用配方法求得三角形面积最大时t的值即可;
(3)如图2所示:过点P作PD⊥OA垂足为D,过圆心O作OE⊥AB,垂足为E.首先证明四边形,四边形OPCE为矩形,然后求得d和r的值即可.
解答 解:(1)k=tan∠COA=tan60°=$\sqrt{3}$.
(2)如图1所示:过点P作PD⊥OA,垂足为D.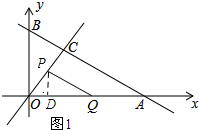
令直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的y=0得:-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$=0,解得x=6,
∴OA=6.
∵∠COA=60°,PD⊥OA,
∴$\frac{PD}{OP}=\frac{\sqrt{3}}{2}$,即$\frac{PD}{t}=\frac{\sqrt{3}}{2}$.
∴PD=$\frac{\sqrt{3}t}{2}$.
${S}_{△OPQ}=\frac{1}{2}OQ•PD$=$\frac{1}{2}×(6-2t)×\frac{\sqrt{3}}{2}t$=-$\frac{\sqrt{3}}{2}$(t2-3t+$(\frac{3}{2})^{2}$-$(\frac{3}{2})^{2}$)=$-\frac{\sqrt{3}}{2}(t-\frac{3}{2})^{2}+\frac{9\sqrt{3}}{8}$,
∴当t=$\frac{3}{2}$时,S有最大值.
(3)如图2所示:过点P作PD⊥OA垂足为D,过圆心O作OE⊥AB,垂足为E.
令直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$的x=0得:y=2$\sqrt{3}$.
∴OB=2$\sqrt{3}$.
∵tan∠BAO=$\frac{OB}{OA}=\frac{2\sqrt{3}}{6}=\frac{\sqrt{3}}{3}$,
∴∠BAO=30°.
∴∠ABO=60°.
∴OC=OBsin60°=2$\sqrt{3}×\frac{\sqrt{3}}{2}$=3.
∵∠COA=60°,
∴∠BOC=30°.
∴∠BOC+∠OBC=90°.
∴∠OCA=90°.
当t=$\frac{3}{2}$时,OD=$\frac{3}{2}×\frac{1}{2}$=$\frac{3}{4}$,PD=$\frac{3}{2}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.DQ=3-$\frac{3}{4}$=$\frac{9}{4}$.
∴tan∠PQO=$\frac{\frac{3\sqrt{3}}{4}}{\frac{9}{4}}$=$\frac{\sqrt{3}}{3}$.
∴∠PQO=30°.
∴∠BAO=∠PQO.
∴PQ∥AB,
∴∠CPQ+∠PCA=180°.
∴∠CPQ=180°-90°=90°.
∴∠ECP=∠CPO=∠OEC=90°.
∴四边形OPCE为矩形.
∴d=OE=PC=OC-OP=3-$\frac{3}{2}$=$\frac{3}{2}$.
PQ=OQsin60°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
∴r=PO=$\frac{1}{2}×\frac{3\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$.
∵d>r.
∴直线AB与以PQ为直径的圆O相离.
点评 本题主要考查的是直线和圆的位置关系、一次函数、矩形的性质和判定、二次函数的最值、锐角三角函数的综合应用,求得d和r的值是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
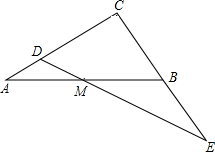 如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.
如图,已知△ABC,∠ACB=90°,BC=AC=1,M为边AB中点,D为AC边上任意一点,联结DM并延长与CB延长线交于点E.设AD=x,BE=y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )| A. | ∠α+∠β+∠γ=180° | B. | ∠α+∠β-∠γ=180° | C. | ∠β+∠γ-∠α=180° | D. | ∠α-∠β+∠γ=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线y=x2-x-6与x轴交于点A、B(A在B的左边),与y轴分别交于点C.
抛物线y=x2-x-6与x轴交于点A、B(A在B的左边),与y轴分别交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种货车辆数(辆) | 2 | 5 |
| 乙种货车辆数(辆) | 3 | 6 |
| 累计运货吨数(吨) | 15.5 | 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com