练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    6×7×8+7×8×9+8×9×10+…+20×21×22=


    1. A.
      52710
    2. B.
      210840
    3. C.
      26355
    4. D.
      105420
    A
    分析：由于（n-1）n（n+1）=[（n-1）n（n+1）（n+2）-（n-2）（n-1）n（n+1）]，利用这个等式可以把所求的题目变为（6×7×8×9-5×6×7×8+7×8×9×10-6×7×8×9+…+20×21×22×23-19×20×21×22），然后化简即可求解．
    解答：∵（n-1）n•（n+1）=[（n-1）n（n+1）（n+2）-（n-2）（n-1）n（n+1）]，
    ∴原式=（6×7×8×9-5×6×7×8+7×8×9×10-6×7×8×9+…+20×21×22×23-19×20×21×22）
    =（20×21×22×23-5×6×7×8 ）
    =52710．
    点评：此题主要考查了有理数地方混合运算，解题的关键是利用（n-1）n（n+1）=[（n-1）n（n+1）（n+2）-（n-2）（n-1）n（n+1）]把题目变形，然后利用有理数混合运算法则计算即可解决问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：单选题

    下列说法正确的是


    1. A.
      0是最小的有理数
    2. B.
      0的相反数还是0
    3. C.
      0的倒数是0
    4. D.
      0除以任何数得0

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    如图，已知一次函数y=kx+b和y=mx+n的图象交于点P，则根据图象可得不等式组0＜mx+n＜kx+b的解集是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    已知关于x的一元二次方程3ax2-bx-2=0和ax2+2bx-6=0有共同的根x=-2，则4a+3b的值为


    1. A.
      4
    2. B.
      -4
    3. C.
      2
    4. D.
      -2

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    下列说法正确的是


    1. A.
      各有一个角是100°的两个等腰三角形相似
    2. B.
      各有一个角是45°的两个等腰三角形相似
    3. C.
      有两边对应成比例的两个等腰三角形相似
    4. D.
      两腰对应成比例的两个等腰三角形相似

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    不等式组数学公式的解集为


    1. A.
      -1＜x≤1
    2. B.
      -1≤x＜1
    3. C.
      -1＜x＜1
    4. D.
      x＜-1或x≥1

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    将两张完全一样的矩形纸条交叉重叠在一起，重叠部分组成的四边形一定是


    1. A.
      正方形
    2. B.
      长方形
    3. C.
      菱形
    4. D.
      无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

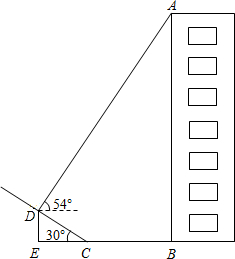    如图，某小区楼房附近有一个斜坡，小张发现楼房在水平地面与斜坡处形成的投影中，在斜坡上的影子长CD=6m，坡角到楼房的距离CB=8m．在D点处观察点A的仰角为54°，已知坡角为30°，你能求出楼房AB的高度吗？（tan54°≈1.38，结果精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    在平面内，到三角形三边距离相等的点是


    1. A.
      三角形两边垂直平分线的交点
    2. B.
      三角形两内角平分线的交点
    3. C.
      三角形两边中线的交点
    4. D.
      以上均不对

    查看答案和解析>>

    同步练习册答案