
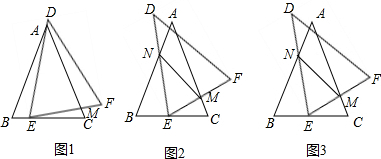
分析 (1)欲证明△ABE∽△ECM,只要证明∠B=∠ECM,∠BAE=∠CEM.
(2)结论正确.先证明△BNE∽△CEM,得$\frac{NE}{EM}$=$\frac{BE}{CM}$,因为BE=EC,所以$\frac{NE}{EM}$=$\frac{EC}{CM}$,即$\frac{NE}{EC}$=$\frac{EN}{CM}$,因为∠NEM=∠C,即可证明△NEM∽△ECM.
(3)结论:直线MN与⊙E相切.如图3中,设⊙E与AB相切于点G,作EH⊥NM于H.首先证明∠ENB=∠ENM,再根据角平分线的性质定理即可证明.
解答 (1)证明:如图1中,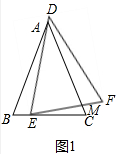
∵△ABC≌△DEF,
∴∠B=∠DEF,
∵AB=AC,
∴∠B=∠ECM,
∵∠AEC=∠B+∠BAE=∠DEF+∠CEM,
∴∠CEM=∠BAE,
∴△ABE∽△ECM.
(2)结论正确.
理由:如图2中,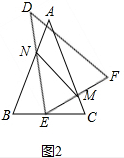
∵∠NEC=∠B+∠ENB=∠NEF+∠CEM,∠NEF=∠B,
∴∠ENB=∠CEM,∵∠B=∠ECM,
∴△BNE∽△CEM,
∴$\frac{NE}{EM}$=$\frac{BE}{CM}$,∵BE=EC,
∴$\frac{NE}{EM}$=$\frac{EC}{CM}$,
∴$\frac{NE}{EC}$=$\frac{EN}{CM}$,∵∠NEM=∠C,
∴△NEM∽△ECM.
(3)结论:直线MN与⊙E相切.
理由:如图3中,设⊙E与AB相切于点G,作EH⊥NM于H.
由(2)可知△BNE∽△CEM,△NEM∽△ECM.
∴∠BNE=∠CEN=∠ENM,
∵AB是⊙E的切线,
∴EG⊥NB,∵EH⊥NM,
∴EG=EH,
∴NM是⊙E的切线.
点评 本题考查全等三角形的性质、相似三角形的判定和性质、圆、角平分线的性质定理等知识,解题的关键是熟练掌握相似三角形的判定和性质,学会利用角平分线的性质定理添加辅助线,属于中考压轴题.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
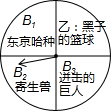 周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)
周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
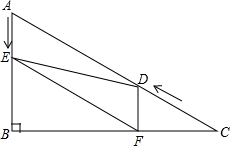 如图,在Rt△ABC中,∠B=90°,AB=3,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AB=3,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
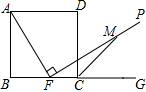 如图,F是正方形ABCD的边BC上的一个点(F与B,C两点不重合),过点F作射线FP⊥AF,∠DCG的平分线交FP于M,求证:AF=FM.
如图,F是正方形ABCD的边BC上的一个点(F与B,C两点不重合),过点F作射线FP⊥AF,∠DCG的平分线交FP于M,求证:AF=FM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com