

分析 (1)画直角△ABC,使得两直角边为1与3,斜边即为所求;
(2)画菱形ABCD,使得边长AB为$\sqrt{5}$.
解答 解:(1)如图所示:
△ABC中,AC=3,BC=1,∠ACB=90°,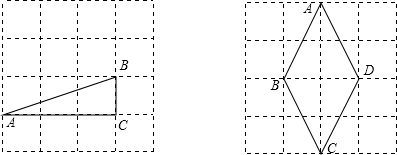 由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{10}$,
直角△ABC即为所求;
(2)如图所示:
∵AC⊥BD,
∴AB=BC=CD=DA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴四边形ABCD是菱形,
∴菱形ABCD即为所求.
点评 本题考查了作图-复杂作图、勾股定理、勾股定理的逆定理以及菱形的判定;熟练掌握勾股定理,并能进行推理计算与作图是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 进价(元/台) | 售价(元/台) | |
| 电饭煲 | 200 | 250 |
| 电压锅 | 160 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制出如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵及以上的人数占总人数的( )
单位在植树节派出50名员工植树造林,统计每个人植树的棵树之后,绘制出如图所示的频数分布直方图(图中分组含最低值,不含最高值),则植树7棵及以上的人数占总人数的( )| A. | 40% | B. | 70% | C. | 76% | D. | 96% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com