
【题目】探索题:图a是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形. 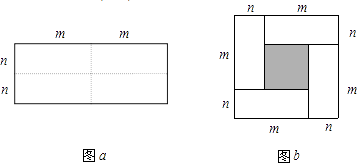
(1)请用两种不同的方法,求图b中阴影部分的面积:方法1:; 方法2:;
(2)观察图b,写出代数式(m+n)2 , (m﹣n)2 , mn之间的等量关系,并通过计算验证;
(3)根据(2)题中的等量关系,解决如下问题:若2a+b=5,ab=2,求(2a﹣b)2的值.
【答案】
(1)(m﹣n)2;(m+n)2﹣4mn
(2)解:(m﹣n)2=(m+n)2﹣4mn;
验证:∵(m﹣n)2=m2﹣2mn+n2,
(m+n)2﹣4mn=m2+2mn+n2﹣4mn=m2﹣2mn+n2,
∴(m﹣n)2=m2﹣2mn+n2
(3)解:∵(2a﹣b)2=(2a+b)2﹣8ab,
∴当2a+b=5,ab=2时,(2a﹣b)2=52﹣8×2=9
【解析】(1)方法1:图b中的阴影部分的正方形的边长等于长为m,宽为n的长方形的长宽之差,即m﹣n,故阴影部分面积为(m﹣n)2; 方法2:图b中的阴影部分的正方形面积等于大正方形的面积减去4个长方形的面积,即(m+n)2﹣4mn;
所以答案是:(m﹣n)2 , (m+n)2﹣4mn;


科目:初中数学 来源: 题型:
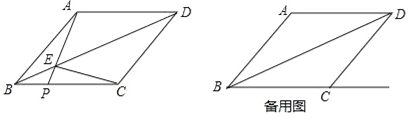
【题目】已知:如图,在菱形ABCD中,AB=5,联结BD,sin∠ABD=![]() .点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
.点P是射线BC上的一个动点(点P不与点B重合),联结AP,与对角线BD相交于点E,联结EC.
(1)求证:AE=CE;
(2)当点P在线段BC上时,设BP=x,△PEC的面积为y,求y关于x的函数解析式,并写出它的定义域;
(3)当点P在线段BC的延长线上时,若△PEC是直角三角形,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
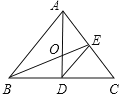
【题目】如图,△ABC的角平分线AD、中线BE相交于点O,则①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线的结论中正确的有_________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
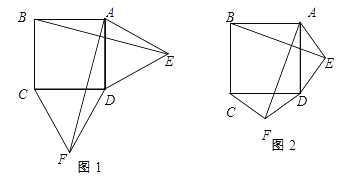
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2x2x7+3x5x4﹣xx8
(2)(m+3)(m﹣3)﹣(m+3)2
(3)(π﹣3)0﹣( ![]() )﹣1+(﹣5)3÷(﹣5)2
)﹣1+(﹣5)3÷(﹣5)2
(4)(1+2x﹣y)(2x+y﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生甲与学生乙学习概率初步知识后设计了如下游戏:学生甲手中有6,8,10三张扑克牌,学生乙手中有5,7,9三张扑克牌,每人从各自手中取一张牌进行比较,数字大的为本局获胜,每次获取的牌不能放回.
(1)若每人随机取手中的一张牌进行比较,请列举出所有情况;
(2)并求学生乙本局获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校有一个长为25m,宽为12m的长方体游泳池,当前水位是0.1m. 现往游泳池注水,水位每小时上升0.3m.
(1) 写出游泳池水深d(m)与注水时间x(h)的函数表达式;
(2) 如果x(h)共注水y(m3),求y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防控冬季呼吸道疾病,我校积极进行校园环境消毒工作,购买了甲、乙两种消毒液共100瓶,其中甲种每瓶6元,乙种每瓶9元,如果购买这两种消毒液共花去780元,求甲、乙两种消毒液各购买了多少瓶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com