
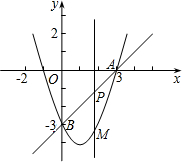
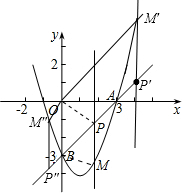
 ��2011•��������ͼ����ƽ��ֱ������ϵ�У�������y=x2+mx+n������A��3��0����B��0��-3������P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ��߽��������ڵ�M�����P�ĺ�����Ϊt��
��2011•��������ͼ����ƽ��ֱ������ϵ�У�������y=x2+mx+n������A��3��0����B��0��-3������P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ��߽��������ڵ�M�����P�ĺ�����Ϊt��| 3 |
| 2��(-1) |
| 3 |
| 2 |
| 0-9 |
| 4��(-1) |
| 9 |
| 4 |
| 9 |
| 4 |
|
|
|
|
| 3 |
| 2��(-1) |
| 3 |
| 2 |
| 0-9 |
| 4��(-1) |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
| 9 |
| 4 |
3+
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |


 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
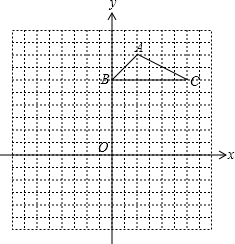 ��2011•��������ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���ABC�Ķ��㶼�ڸ���ϣ�����ƽ��ֱ������ϵ��
��2011•��������ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���ABC�Ķ��㶼�ڸ���ϣ�����ƽ��ֱ������ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �ڵ�B��
�ڵ�B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
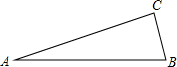 ��2011•��������ͼ���ڡ�ABC�У���ACB=90�㣬��A=15�㣬AB=8����AC•BC��ֵΪ��������
��2011•��������ͼ���ڡ�ABC�У���ACB=90�㣬��A=15�㣬AB=8����AC•BC��ֵΪ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2011•��������ͼ����Բ�εĵ��ݶѶ���P����һֻè����������Բ���ϵĵ�A����һֻ����è����ĸ��PA��ȥץ����è�����Aʱ�����������ŵ���Բ�����ܣ�è�ں���������ͬ��·������Բ�ܵĵ�B��ץ�����������ĸ��BP�ص�����P��������������У�����è���ٶ������ٵģ�è���������P����s������ʱ��Ϊt����s��t֮��ĺ�����ϵͼ���ǣ�������
��2011•��������ͼ����Բ�εĵ��ݶѶ���P����һֻè����������Բ���ϵĵ�A����һֻ����è����ĸ��PA��ȥץ����è�����Aʱ�����������ŵ���Բ�����ܣ�è�ں���������ͬ��·������Բ�ܵĵ�B��ץ�����������ĸ��BP�ص�����P��������������У�����è���ٶ������ٵģ�è���������P����s������ʱ��Ϊt����s��t֮��ĺ�����ϵͼ���ǣ��������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com