
【题目】如图,在![]() 中,
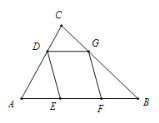
中,![]() ,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
,AB=5,BC=4,点D为边AC上的动点,作菱形DEFG,使点E、F在边AB上,点G在边BC上.若这样的菱形能作出两个,则AD的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图(1)是某公园里的一种健身器材,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,若AC∥EF,试判断线段KG、KD、GE间的数量关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中线段AB表示某工程的部分隧道,无人勘测飞机从隧道的一侧点A出发,沿着坡度为1:1.5的路线AE飞行,飞行至分界点C的正上方点D时,测得隧道另一侧点B的俯角为23°,继续飞行至点E,测得点B的俯角为45°,此时点E离地面的高度EF=800米.
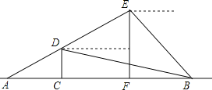
(1)分别求隧道AC和BC段的长度;
(2)建工集团安排甲、乙两个金牌施工队分别从隧道两头向中间施工,甲队负责AC段施工,乙队负责BC段施工,乙每天的工作量是甲的2倍,两队同时开工5天后,甲队将速度提高25%,乙队将速度提高了150%,从而两队同时完成,求原计划甲、乙两队每天各施工多少米.(参考数据:tan23°≈0.4,cos23°≈0.9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某科技物展览大厅有A、B两个入口,C、D、E三个出口.小昀任选一个入口进入展览大厅, 参观结束后任选一个出口离开.
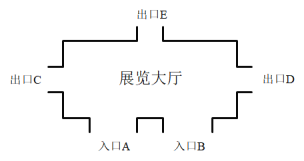
(1)若小昀已进入展览大厅,求他选择从出口C离开的概率.
(2)求小昀选择从入口A进入,从出口E离开的概率.(请用列表或画树状图求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,有一块含有30°的直角三角形![]() 的直角边
的直角边![]() 的长恰与另一块等腰直角三角形
的长恰与另一块等腰直角三角形![]() 的斜边
的斜边![]() 的长相等.把该套三角板放置在平面直角坐标系中,且
的长相等.把该套三角板放置在平面直角坐标系中,且![]()
(1)若某开口向下的抛物线的顶点恰好为点![]() ,请写出一个满足条件的抛物线的解析式.
,请写出一个满足条件的抛物线的解析式.
(2)若把含30°的直角三角形绕点![]() 按顺时针方向旋转后,斜边
按顺时针方向旋转后,斜边![]() 恰好与轴重叠,点
恰好与轴重叠,点![]() 落在点
落在点![]() ,试求图中阴影部分的面积(结果保留
,试求图中阴影部分的面积(结果保留![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请直接写出m的值为_________.
(2)求出这个二次函数的解析式.
(3)当![]() 时,则y的取值范围为______________________________.
时,则y的取值范围为______________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com