
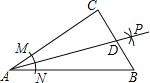
【题目】如图,在Rt△ABC中,∠C=90°,以A为圆心,以任意长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,以一个定长为半径画弧,两弧交于点P,作射线AP交BC于点D.若AC=8,BC=6,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过点D作DE⊥AB于点E,由作图方法可知AP是∠BAC的平分线;由角平分线的性质定理可得CD=DE;由勾股定理求得AB的长;判定Rt△ADC≌Rt△ADE(HL);设CD=DE=x,在Rt△DEB中,由勾股定理求得x的值即可.
解:过点D作DE⊥AB于点E,如图所示:

∵∠C=90°,由作图方法可知AP是∠BAC的平分线,
∴CD=DE,设CD=DE=x,
在Rt△ABC中,
∵AC=8,BC=6,
∴AB=10.
∵∠C=∠AED=90°,AD=AD,DC=DE,
∴Rt△ADC≌Rt△ADE(HL),
∴AC=AE=8,
∴EB=2,
在Rt△DEB中,
∵BD2=DE2+BE2,
∴(6﹣x)2=x2+22,
解得:x=![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,四边形ABCD四个顶点的坐标分别为A(-2,0),B(-1,2),C(3,3),D(4, 0).
(1)画出四边形ABCD;
(2)把四边形ABCD向下平移4个单位长度,再向左平移2个单位长度得到四边形A′B′C′D′,画出四边形A′B′C′D′,并写出C′的坐标。
(3)求出四边形ABCD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
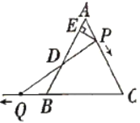
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
(1)若![]() 时,求
时,求![]() 的长;
的长;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C:y=![]() x2+bx+c 交
x2+bx+c 交 ![]() 轴于点A(0,-1)且过点
轴于点A(0,-1)且过点 ![]() , P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
, P是抛物线C上一个动点,过P作PB∥OA,以P为圆心,2为半径的圆交PB于C、D两点(点D位于点C下方).
(1)求抛物线C的解析式;
(2)连接AP交⊙P于点E,连接DE,AC.若ΔACP是以CP为直角边的直角三角形,求∠EDC的度数;
(3)若当点P经过抛物线C上所有的点后,点D随之经过的路线被直线 ![]() 截得的线段长为8,求
截得的线段长为8,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸.如图,已知圆筒高108cm,其圆筒底面周长为36cm,如果在表面缠绕油纸4圈,应裁剪油纸的最短为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
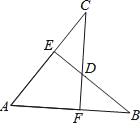
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.
以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com