
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
【答案】(1)见解析;(2)3
【解析】
(1)根据根的判别式的符号来证明;
(2)根据韦达定理得到b+c=2k+1,bc=4k-3.又在直角△ABC中,根据勾股定理,得(b+c)2﹣2bc=(![]() )2,由此可以求得k的值.
)2,由此可以求得k的值.
(1)证明:∵△=[﹣(2k+1)]2﹣4×1×(4k﹣3)=4k2﹣12k+13=(2k﹣3)2+4,
∴无论k取什么实数值,总有=(2k﹣3)2+4>0,即△>0,
∴无论k取什么实数值,该方程总有两个不相等的实数根;
(2)解:∵两条直角边的长b和c恰好是方程x2﹣(2k+1)x+4k﹣3=0的两个根,得
∴b+c=2k+1,bc=4k﹣3,
又∵在直角△ABC中,根据勾股定理,得
b2+c2=a2,
∴(b+c)2﹣2bc=(![]() )2,即(2k+1)2﹣2(4k﹣3)=31,
)2,即(2k+1)2﹣2(4k﹣3)=31,
整理后,得k2﹣k﹣6=0,解这个方程,得k=﹣2或k=3,
当k=﹣2时,b+c=﹣4+1=﹣3<0,不符合题意,舍去,当k=3时,b+c=2×3+1=7,符合题意,故k=3.


科目:初中数学 来源: 题型:
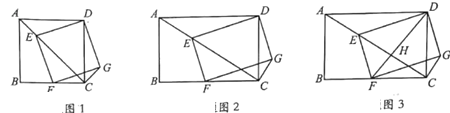
【题目】在矩形ABCD中,AB=a,AD=b,点E为对角线AC上一点,连接DE,以DE为边,作矩形DEFG,点F在边BC上;
(1)观察猜想:如图1,当a=b时,![]() =______,∠ACG=______;
=______,∠ACG=______;
(2)类比探究:如图2,当a≠b时,求![]() 的值(用含a、b的式子表示)及∠ACG的度数;
的值(用含a、b的式子表示)及∠ACG的度数;
(3)拓展应用:如图3,当a=6,b=8,且DF⊥AC,垂足为H,求CG的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个3×2的矩形(即长为3,宽为2)可以用两种不同的方式分割成3或6个边长是正整数的小正方形,即:小正方形的个数最多是6个,最少是3个.

(1)一个5×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(2)一个7×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个;
(3)一个(2n+1)×2的矩形用不同的方式分割后,小正方形的个数最多是 个,最少是 个.(n是正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
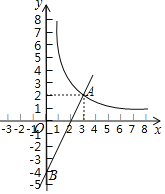
(1)求函数![]() 和y=kx+b的解析式;
和y=kx+b的解析式;
(2)结合图象直接写出不等式组0<![]() <kx+b的解集.
<kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
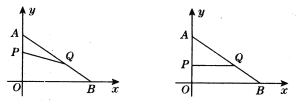
(1)求直线AB的解析式;
(2)当t为何值时,△APQ与△AOB相似?
(3)当t为何值时,△APQ的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世园会开园期间,为了满足不同人群的游览需求,组委会倾情打造了四条趣玩路线,分别是“解密世园会”、“爱我家,爱园艺”、“园艺小清新之旅”和“快速车览之旅”小明一家想通过抽签的方法选择其中的两条路线进行游玩,于是他们制作了如下四张卡片,然后从四张卡片中随机抽取其中的两张若小明最钟爱的游玩路线是“园艺小清新之旅",小明的爸爸和妈妈最钟爱的游玩路线是“解密世园会”,请用列表法或画树状图法求出:他们同时抽中“园艺小清新之旅”和“解密世园会”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,顶点为
,顶点为![]() .
.
(1)求这条抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)点![]() 关于抛物线对称轴的对应点为点
关于抛物线对称轴的对应点为点![]() ,联结
,联结![]() ,求
,求![]() 的正切值;
的正切值;
(3)将抛物线![]() 向上平移
向上平移![]() 个单位,使顶点
个单位,使顶点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,如果
处,如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
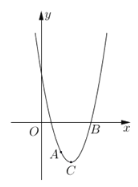
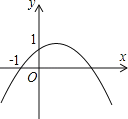
【题目】如图,二次函数y=ax2+bx+c(a#0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0;②b2>4ac;③0<b<1;④当x<﹣1时,y<0.其中正确结论的个数是( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商业集团新建一小车停车场,经测算,此停车场每天需固定支出的费用(设施维修费、车辆管理人员工资等)为800元.为制定合理的收费标准,该集团对一段时间每天小车停放辆次与每辆次小车的收费情况进行了调查,发现每辆次小车的停车费不超过5元时,每天来此处停放的小车可达1440辆次;若停车费超过5元,则每超过1元,每天来此处停放的小车就减少120辆次.为便于结算,规定每辆次小车的停车费x(元)只取整数,用y(元)表示此停车场的日净收入,且要求日净收入不低于2512元.(日净收入=每天共收取的停车费﹣每天的固定支出)
(1)当x≤5时,写出y与x之间的关系式,并说明每辆小车的停车费最少不低于多少元;
(2)当x>5时,写出y与x之间的函数关系式(不必写出x的取值范围);
(3)该集团要求此停车场既要吸引客户,使每天小车停放的辆次较多,又要有较大的日净收入.按此要求,每辆次小车的停车费应定为多少元?此时日净收入是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com