
 ),则四边形ABCD的面积的最大值与最小值的差为___ ___.
),则四边形ABCD的面积的最大值与最小值的差为___ ___. 
 ﹣4.
﹣4.
 ),
), ,OF=1,
,OF=1, ,CF=
,CF=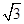 ,
, +1,DM=
+1,DM= ﹣1,AM=
﹣1,AM=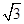 ﹣
﹣ ,CM=
,CM=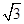 +
+ ,
,
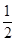 ×4
×4 ,
, ;
;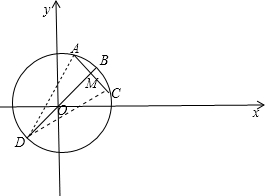
 )
)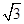 ,MC=1,根据垂径定理,AC=2MC=2,
,MC=1,根据垂径定理,AC=2MC=2,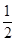 AC•BM+
AC•BM+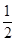 AC•DM=
AC•DM=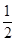 AC•BD=4.
AC•BD=4. ﹣4).
﹣4). ﹣4.
﹣4.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
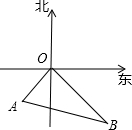
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,求OD的长.
,求OD的长.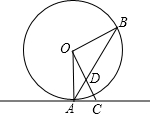
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
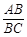 =k.
=k.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
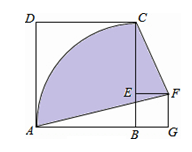
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com