
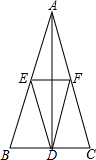
 如图.在△ABC中,AB=AC,AD平分∠BAC交BC于点D,E,F分别是AB,AC的中点,△DEF是等腰三角形吗?请说明理由.
如图.在△ABC中,AB=AC,AD平分∠BAC交BC于点D,E,F分别是AB,AC的中点,△DEF是等腰三角形吗?请说明理由. 分析 由等腰△ABC,根据等边对等角,得到∠B=∠C,由平行线的性质得到角相等,由等量代换得到∠AEF=∠AFE,证得AE=AF,由等腰三角形的三线合一的性质证得AD是EF的中垂线,由中垂线的性质得到结论.
解答 解:△DEF是等腰三角形,
∵AB=AC,
∴∠B=∠C,
∵E,F分别是AB,AC的中点,
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∵AB=AC,AD平分∠BAC交BC于点D,
∴AD⊥BC,
∴AD⊥EF,
∴AD垂直平分EF,
∴DE=DF,
∴△DEF是等腰三角形.
点评 本题主要考查了平行线的性质,等腰三角形的判定,线段垂直平分线的判定和性质,解决本题的关键是熟记等腰三角形的判定.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:选择题
| 尺寸 | S | M | L | XL | XXL |
| 数量(件) | 50 | 110 | 150 | 80 | 70 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在高度为2.8m的一面墙上,准备开凿一个矩形窗户,现用9.5m长的铝合金条制成如图所示的窗框,设宽为xm,窗户的透光面积为ym2
在高度为2.8m的一面墙上,准备开凿一个矩形窗户,现用9.5m长的铝合金条制成如图所示的窗框,设宽为xm,窗户的透光面积为ym2查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com