
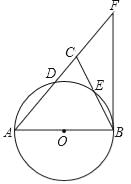
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,以AB为直径的⊙O分别交AC、BC于点D、E,过点B作直线BF,交AC的延长线于点F.
(1)求证:BE=CE;
(2)若AB=6,求弧DE的长;
(3)当∠F的度数是多少时,BF与⊙O相切,证明你的结论.
【答案】(1)证明见解析;(2)弧DE的长为![]() π;(3)当∠F的度数是36°时,BF与⊙O相切.理由见解析.
π;(3)当∠F的度数是36°时,BF与⊙O相切.理由见解析.
【解析】
(1)连接AE,求出AE⊥BC,根据等腰三角形性质求出即可;
(2)根据圆周角定理求出∠DOE的度数,再根据弧长公式进行计算即可;
(3)当∠F的度数是36°时,可以得到∠ABF=90°,由此即可得BF与⊙O相切.
(1)连接AE,如图,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE;
(2)∵AB=AC,AE⊥BC,
∴AE平分∠BAC,
∴∠CAE=![]() ∠BAC=
∠BAC=![]() ×54°=27°,
×54°=27°,
∴∠DOE=2∠CAE=2×27°=54°,
∴弧DE的长=![]() ;
;
(3)当∠F的度数是36°时,BF与⊙O相切,
理由如下:∵∠BAC=54°,
∴当∠F=36°时,∠ABF=90°,
∴AB⊥BF,
∴BF为⊙O的切线.


科目:初中数学 来源: 题型:
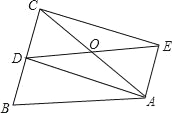
【题目】如图,在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形.
(1)求证:四边形ADCE是矩形;
(2)若AC、DE交于点O,四边形ADCE的面积为16![]() ,CD=4,求∠AOD的度数.
,CD=4,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
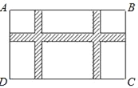
【题目】如图,某小区规划在长20米,宽10米的矩形场地ABCD上修建三条同样宽的小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为162米2,问小路应为多宽?
查看答案和解析>>
科目:初中数学 来源: 题型:
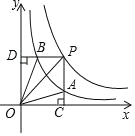
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B.下面结论:
的图象于点B.下面结论:
①PA与PB始终相等;②△OBP与△OAP的面积始终相等;
③四边形PAOB的面积不变;④PABD=PBAC.
其中一定正确的是_____(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
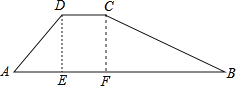
【题目】水库大坝截面的迎水坡坡比(DE与AE的长度之比)为1:0.6,背水坡坡比为1:2,大坝高DE=30米,坝顶宽CD=10米,求大坝的截面的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
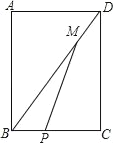
【题目】如图所示,矩形ABCD中,AB=8,BC=6,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
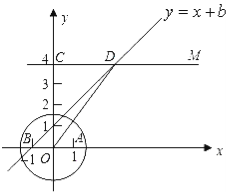
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com