
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
|
x(单位:台) |
10 |
20 |
30 |
|
y(单位:万元∕台) |
60 |
55 |
50 |
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
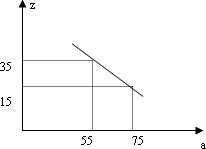
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)

解:(1)设y与x之间的关系式为y=kx+b,由题意,得
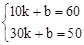 ,解得:
,解得: 。
。
∴y= x+65。
x+65。
∵该机器生产数量至少为10台,但不超过70台,∴10≤x≤70。
(2)由题意,得xy=2000,即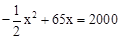 ,即
,即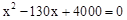 。
。
解得:x1=50,x2=80>70(舍去)。
答:该机器的生产数量为50台。
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为 ,由函数图象,得
,由函数图象,得
 ,解得:
,解得: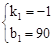 。
。
∴z=﹣a+90。
当z=25时,a=65;当x=50时,y=40,
∴总利润为:25(65﹣40)=625(万元).。
答:该厂第一个月销售这种机器的利润为625万元
【解析】
试题分析:(1)设y与x之间的关系式为y=kx+b,运用待定系数法就可以求出其关系式,由该机器生产数量至少为10台,但不超过70台就可以确定自变量的取值范围。
(2)根据每台的成本乘以生产数量等于总成本建立方程求出其解即可。
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ka+b,运用待定系数法求出其解析式,再将z=25代入解析式求出a的值,就可以求出每台的利润,从而求出总利润。


科目:初中数学 来源: 题型:
 (2013•临沂)某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
(2013•临沂)某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
查看答案和解析>>
科目:初中数学 来源:2013年山东省临沂市高级中等学校招生考试数学 题型:044
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元/台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |
查看答案和解析>>
科目:初中数学 来源:2013年山东省临沂市中考数学试卷(解析版) 题型:解答题
| x(单位:台) | 10 | 20 | 30 |
| y(单位:万元∕台) | 60 | 55 | 50 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com