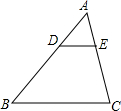
如图.△ABC中.DE∥BC.$\frac{AD}{AB}$=$\frac{1}{3}$.DE=3.则BC边的长是( )A．6B．7C．8D．9 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

15．

如图，△ABC中，DE∥BC，$\frac{AD}{AB}$=$\frac{1}{3}$，DE=3，则BC边的长是（　　）

A．

B．

C．

D．

分析由DE∥BC可得到DE：BC=AD：AB，由$\frac{AD}{AB}$=$\frac{1}{3}$，DE=3，即可BC的长．

解答解：∵DE∥BC，
∴△ADE∽△ABC，
∴DE：BC=AD：AB=1：3，
∵DE=3，
∴BC=9．
故选：D．

点评本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

6．

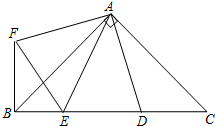如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB连接EF，证明：△AED≌△AEF．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

7．下列事件中，属于随机事件的是（　　）

	A．	$\sqrt{63}$的值比8大
	B．	购买一张彩票，中奖
	C．	地球自转的同时也在绕日公转
	D．	袋中只有5个黄球，摸出一个球是白球

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．如图（1），在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C（0，m），A（n，m），且（m-4）²+n²-8n=-16，过C点作∠ECF分别交线段AB、OB于E、F两点．

（1）求A点的坐标；
（2）若OF+BE=AB，求证：CF=CE；
（3）如图（2），若∠ECF=45°，给出两个结论：?OF+AE-EF的值不变；?OF+AE+EF的值不变，其中有且只有一个结论正确，请你判断出正确的结论，并加以证明和求出其值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．

如图，在Rt△ABC中，∠ACB=90°，∠B=30°，将△ABC绕点C按顺时针方向旋转n度后，得到△DEC，点D刚好落在AB边上，DE交BC于点O．
（1）求n的值；
（2）若F是DE的中点，求证：△ABC∽△FCO．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

20．若-4≤a≤0，则代数式$\sqrt{9+6a+{a}^{2}}$+$\sqrt{{a}^{2}-10a+25}$的最大值为10．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

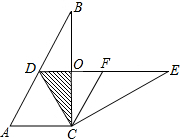
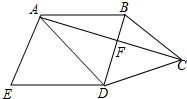如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC．
（1）求证：四边形ABDE是平行四边形；
（2）如果DA平分∠BDE，AB=5，AD=6，求AC的长．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．有一项工程，由甲、乙两个工程队合作完成，工作一段时间后，乙队改进了技术，提高了工作效率．设甲的工作量为y_甲（米），乙的工作量为y_乙（米），甲、乙合作完成的工作量为y（米），工作时间为x（时）．y_甲与x之间的部分函数图象如图①所示，y与x之间的部分函数图象如图②所示．
（1）则乙队2天、6天的工作量分别为40；160．
（2）当2≤x≤6时，求y_乙与x的函数关系式；当0≤x≤6时，在图①中画出y_乙与x之间的函数图象．
（3）工作第4天时，甲、乙两队共完成的工作量为200米．
（4）若6天后，乙保持第6天的工作效率，甲改进了技术，提高了工作效率，当x=8时，甲乙之间的工作量相差10米，求甲提高工作效率后平均每天完成多少米？

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．已知$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$是方程组$\left\{\begin{array}{l}{|x|=2}\\{2x+y=3}\end{array}\right.$的解，则a+b等于（　　）

A．

B．

C．

1或5

D．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学